Juggling: Theory and Practice
by Colin Wright
Juggling has fascinated people for centuries. Seemingly oblivious
to gravity, the skilled practitioner will keep several objects in
the air at one time, and weave complex patterns that seem to defy
analysis. As the first known depiction of jugglers dates back
nearly 4000 years, it's hard to imagine there's anything new
to learn.
But a lesson we've learned from Martin Gardner is that there's
always something new to learn, always something new to discover.
So let's start with a quick review of classical juggling, and then
see what new things we found, partly by accident, partly by hard
work, and mostly because with mathematics we can see things that
are otherwise hidden.
We start by describing briefly the classic juggling patterns.
The Standard Pattern
|
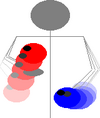
The most common misconception is that when we juggle, the balls go
round in a (highly elongated) circle.
Juggling the balls in a cycle like this requires that every time a
ball is thrown it must be handled by each hand (and
therefore at most twice for all but the exceptionally gifted).
In particular, the hands do different things. One hand
catches the ball and shunts it over, the other hand receives the
ball and then launches it into the air.
|
|
|
Exercise: ignoring air resistance, what are the paths
of the balls? Warning: It's not a parabola. |
|
Anyone who tries this with two balls will launch with their dominant
hand, showing clearly that when juggling the throw is critically
important, not the catch. If the throw is perfect, the catch will
take care of itself.
So what happens if we ask that each hand does the same thing, and
each ball does the same thing (as each other ball, not the same as
the hands. That would be silly).
Firstly, each ball must be thrown in turn.
If not, then one ball must have overtaken another, so their
throws aren't the same. If we're juggling n balls, and each
ball is thrown in turn, it then becomes clear that there are two
distinct cases: either the number of balls is divisible by the
number of hands, or it isn't.
|
Concentrating on the case of the juggler with exactly
two hands, that give us two distinct cases: an even number of
balls, and an odd number of balls.
If we're juggling an even number of balls, and the balls are all
thrown in turn, each ball will have to stay in the same hand. The
pattern then becomes half the balls in each hand and is referred
to as the "Fountain" pattern. (Pictured here at right.) Although
often regarded by non-jugglers as somehow being akin to cheating,
the analysis above shows that the non-changing of hands is required
by the condition that all throws be the same.
|
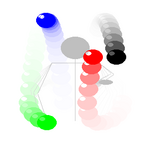
Four ball fountain
|
|
|
Equally, if we're juggling an odd number of balls, each ball must
be thrown by alternate hands. This leads to a "Lazy-Eight" pattern
known (in English) as the "Cascade". Again, with an odd number of
balls, the condition that every throw be the same requires us
to have each ball changing hands.
These we call the "Standard Pattern" for a given
number of balls. Other conditions are often imposed for
basic patterns, most commonly that throws (and hence catches)
occur in a metronomic rhythm, and throws are made inside
shoulder width, and catches are made outside shoulder width.
Juggling in theory
|
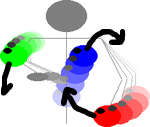
Three ball cascade
|
|
So some simple analysis can tell us things about juggling patterns
that we might otherwise not realise. One of the earliest published
examples of this came from Claude Shannon, the father of Information
Theory. The "Shannon Juggling Theorem" says that when juggling the
standard pattern we have b(d+e) = h(d+f) where
b is the number of balls,
d is the dwell time (the time a ball spends in the hand),
e is empty time of a hand,
h is the number of hands, and
f is the flight time of a throw. [1]
But what about non-standard patterns? There are literally infinitely
many possible variations on a theme. The
throws and catches can be made in many different places, the timing
can be varied, balls can be carried through and around other
balls, multiple balls can be thrown and caught together, and
so on.
|
The possible variations are so great both in style and detail
that it is unsurprising that, despite thousands of years of
history, until the mid-1980s there was no notation for juggling
patterns. Even then the vast array of possibilities seemed
to make the task of devising a notation impossible.
Simplifying juggling
To make progress we simplify the domain of discourse. Specifically,
we assume from here on that throws happen to a metronomic beat, and
that the throws and catches happen just as for the standard pattern.
Further, we assume that we only throw one ball at a time, and we only
catch one ball at a time.
|
Most people who start juggling want to learn four, then five,
and so on. Here is the secret to learning to juggle five - don't
practice five! Instead, practice each required skill separately.
For each skill - hand speed, throw angle accuracy, throw height
accuracy, rate of throw, etc. - find a simpler trick that
requires that skill and practise that trick. After finding and
mastering a trick for each separate skill, putting them together
becomes achievable in a much shorter time than trying to acquire
all the skills
symultaneously
simultaniously
similtayneusly
at the same time. And it's more fun. |
|
We're now left with very few options for finding variations in our
juggling. Specifically, when we throw a ball, the time it spends in
the air is quantised, because it has to come down at one of the
prescribed times for catches. Further, once we know when it comes
down, that controls how high it goes, and where it comes down.
So we describe each throw by a single
number - the time it spends in the air. However, since we don't know
what proportion of time the hands spend full (or empty), it makes
our task easier to think not of the catch,
but of the next throw.
Now we can see that because throws are separated by
a whole number of beats, each ball spends a whole number of beats in its
journey from one throw to the next.
Each throw can be described entirely by this single number.
The magical thing about this number is that when we're juggling
three balls in the standard pattern, each ball is thrown every
third time, so the number to describe the throw is a 3. And
there's nothing special about 3. Whenever we juggle the standard
pattern for n balls, each ball is thrown every
nth
throw.
Back in the mid 1980s it was realised [2] that some of the well-known
juggling tricks could be described completely just by
the appropriate string of numbers to describe the throws. Obviously
when juggling the standard three ball pattern we can write ...3333...
and for 8 balls we can write ...8888... and so on, but there is a
well-known trick with four clubs. Normally juggled with double
spins, throw one club high with a triple spin, and the next club low
with a single, each club changing hands.
Each club drops into the slot vacated by the other, and the pattern then
continues as if nothing happened. Much less impressive when done with balls, it is
a useful exercise to practise the exact
height required for five ball juggling. The high throw will next be
thrown five beats later, so is described as a five. The low throw
is a three, so we can describe a single instance of this trick as
...444_53_444...
Another well-known four ball trick is make two consecutive throws as
if juggling five, pause, and then restart. This can be described as
...444_552_444... (Exercise: why is a momentary hold described as a 2?)
Another variation is to throw all four balls as if
juggling five. Of course, after the first four throws we've run out
of balls, but if we wait for a beat all the balls come down in order
and we can restart our four ball pattern. We write this as
...444_55550_444... It's no surprise that
for that moment when we don't have a ball we describe it as a 0,
although we shall shortly see that this raises some interesting
questions.
Putting it all together ...
|
Collecting these different tricks and writing them one above
the other, putting at the top the uninterrupted four ball fountain,
we end up with this:
... 4 4 4 4 4 4 4 ...
... 4 4 4 5 3 4 4 4 ...
... 4 4 4 5 5 2 4 4 4 ...
... 4 4 4 5 5 5 5 0 4 4 4 ...
The pattern was almost impossible to see when we first wrote
these down, but leaving the gap makes it unmistakable.
The pattern ... 444 5551 444 ... is clearly missing, and based
on the sequence, clearly should be a juggling trick.
But it was a trick we didn't know.
From a four ball fountain throw three balls as if juggling a five ball
cascade. Now you have one ball left - DON'T THROW IT! Zip that ball
across into the otherwise empty hand. Now instead of waiting
for a beat, you can carry on immediately.
|

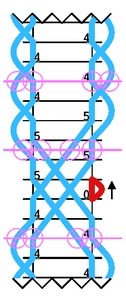
Space-time diagram
for 5551
|
Do this constantly, and suddenly it feels a lot like five balls.
Three out of every four throws is a 5-ball throw, and the pattern
is there, in the air, with just a flicker for a missing ball
every fourth beat. Superb practice for 5, and enormously easier
as it's only four.
An entirely new juggling trick, discovered through mathematics.
A mystery emerges ...
We've shown that some juggling tricks can be described by
sequences of numbers, and that by following patterns we can
find previously unknown tricks. Not all sequences make
valid juggling tricks, but space does not permit investigation
of that particular aspect.
|
There is another question that emerges, however, when we look
at the physical reality. We do, after all, have to hold the
ball between catching and throwing.
In our previous Space-Time
diagram we've made the simple
assumption that the hands are full for exactly half the
time, and we can see that the throws that come back to the
same hand are four beats from throw to throw, three beats in
the air, giving a hold time of one.
The high throws that change
hands are fives, and they spend four beats in the air.
The zip across is no time in the air, one beat in the hand,
and therefore its "Cycle Time" - the time to the next throw -
is 1. All this is just as we might expect.
But what about the 0 in 55550? Every other number is the time
from throw to throw, and the time in the air is one less.
If we follow that pattern, the 0 should give an air-time of
-1. We have predicted the time-travel of a juggling ball.
How can that possibly work??
|
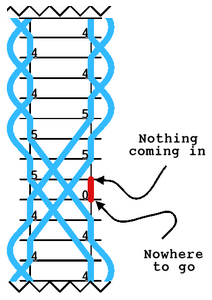
|
|
If the hands are full for half the time we end up with a ball
in the right hand that has come from nowhere, and has nowhere
to go. Clearly we should have the ball go back in time to
become itself, just as required.
If we draw a horizontal line on our diagram it's a single
instant of time, dividing past above from future below. In
a sense it's a photograph, freezing the action and seeing
where things are. The diagram here at left has several
photographs, each showing where all four balls are.
In each case there's a ball in the hand and balls in the air, always
exactly four of them. Which is right and reasonable, as we
are juggling four balls. By the conservation law of juggling
equipment we should always have four balls.
|
|
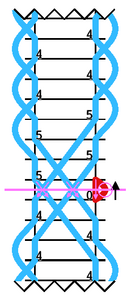
But look at the photograph in the diagram on our right.
Here we have four balls in the air between the hands, and
another ball in the right hand. Clearly there's something
strange happening. But wait! There's more! There's also
a ball going backwards in time. That must count as a negative
ball, to bring our count back to the required four.
It's an anti-ball!
|
We can think of the "catch" (where the ball comes from
the future) as the mutual creation of a ball/anti-ball pair,
and the throw back into the past as the mutual
annihilation. Thus we have confirmed the view in modern
physics that an anti-particle can be thought of as a particle
going backwards in time: a positron is an electron going
backwards in time, an anti-proton is a proton going
backwards in time, etc. More, since a photon is its own
anti-particle it doesn't know whether it's coming or going,
but since it travels at the speed of light, Einstein tells
us time is stopped.
|
|
But
E=mc2,
so where does the energy come from to create a ball/anti-ball
pair? Just as there's a quantum uncertainty principle between
position and momentum, there's also a quantum uncertainty
principle between energy and time. We know exactly
when the throws and catches are happening, so we have a very
small uncertainty in time and we can borrow
from the quantum uncertainty in energy to create a virtual
ball/anti-ball pair. |
|
In truth, the anti-ball can be thought of as subtracting
a ball from where we expect one, leaving us with an empty
hand when our assumptions would normally require a ball.
And in conclusion ...
|
It doesn't end there. Now there are notations for hand movements,
timing variations, patterns involving more than one juggler.
We have arithmetic methods for determining whether a given
sequence can be juggled, and algorithms for producing all
possible juggling sequences with any number of balls. Work
continues to make these newer notations simpler, cleaner,
and more useful.
|
But the real bonus is that this material is being used as
a vehicle to bring the excitement and enthusiasm of
recreational mathematics to thousands each year, year on year.
The juggling is fun, but the maths, as one student said to me,
is "funner".
|
Footnotes / References
- A draft paper for Scientific American is included in
"Claude Elwood Shannon Collected Papers," edited by
N.J.A. Sloane and A. D. Wyner, New York, IEEE Press,
1993, pages 850-864).
- http://www.solipsys.co.uk/new/Juggling.html
- http://www.solipsys.co.uk/new/ColinWright.html
- http://en.wikipedia.org/wiki/Siteswap
- http://www.cecm.sfu.ca/organics/papers/buhler/paper/html/paper.html
The Author
Colin Wright took his B.Sc. at Monash University, Australia,
and his Ph.D. at Cambridge University, UK, both in Pure Mathematics.
These days he is Director of Research at a company which makes
maritime surveillance equipment, still finding time to give
presentations all over the world on "Juggling - Theory and Practice."






