Subscribe!

• Colins Blog

• You Have To Admire Their Optimism
• Representatives Matter
• Pythagoras By Incircle
• A Puzzle About Puzzles
• How Not To Do Twitter
• Calculating 52 Factorial By Hand
• Small Things Might Not Be So Small
• Not If You Hurry
• Factoring Via Graph Three Colouring
• Another Proof Of The Doodle Theorem
• When Obvious Is Not Obvious
• Graph Three Colouring
• The Doodle Theorem
• Be Careful What You Say
• The Mutilated Chessboard Revisited
• A Mirror Copied
• The Other Other Rope Around The Earth
• Photocopy A Mirror
• The Point Of The Banach Tarski Theorem
• Sieve Of Eratosthenes In Python
• Fast Perrin Test
• Russian Peasant Multiplication
• FindingPerrinPseudoPrimes Part2
• FindingPerrinPseudoPrimes Part1
• The Unwise Update
• Miles Per Gallon
• Tracking An Item On Hacker News
• Hacker News User Ages
• Poking The Dusty Corners
• There Is No Time For This
• Publically Sharing Links
• Learning Times Tables
• Graceful Degradation
• Diagramming Maths Topics
• On The Rack
• Square Root By Long Division
• Beyond The Boundary
• Fill In The Gaps
• Software Checklist
• NASA Space Crews
• The Birthday Paradox
• The Trapezium Conundrum
• Revisiting The Ant
• The Ant And The Rubber Band
• Irrationals Exist
• Multiple Choice Probability Puzzle
• Random Eratosthenes
• Wrapping Up Square Dissection
• Dissecting A Square Part 2
• Dissecting A Circle
• Dissecting A Square
• An Oddity In Tennis
• Decision Tree For Tennis
• Decision Trees In Games
• A Matter Of Convention
• Do You Nourish Or Tarnish
• Binary Search Reconsidered
• Two Equals Four
• The Lost Property Office
• The Forgiving User Interface
• Setting Up RSS
• Withdrawing From Hacker News

• Random Writings.
• Colins Blog 2010
• Colins Blog 2009
• Colins Blog 2008
• Colins Blog 2007
• Colins Blog Before 2007

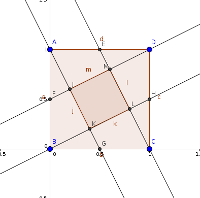
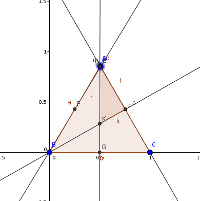
2016/09/18 - An Unexpected Fraction

On 2016-09-09, @MEIMaths tweeted an image and said:

Quadrilateral Problem

The way the question is phrased makes you feel two things.

Firstly, you have to feel that the answer is likely to be surprising in some way, so that means it's likely to be a nice puzzle.

But secondly, it seems clear from the phrasing that the answer must be the same regardless of the particular quadrilateral chosen.

Well, I've seen this before in the context of a square, and the answer there is lovely - it's a fifth. The proof in the case of a square is fairly simple, and there are a number of ways of going about it. So there we are, it's sorted, the answer is a fifth.

Nice one.

Quadrilateral Problem The Square case

But then Hugh Hunt sent me an email saying:

Quadrilateral Problem Limiting Triangle

That's a good question. If we take two adjacent vertices of the square and move them together, just before they meet we do still have a convex quadrilateral, so because we expect the answer to be constant (because of the context) we would expect the answer still to be a fifth, but the answer is now pretty obviously a sixth.

So what's going on?

The short answer seems to be that @MEIMaths mis-spoke themselves, and despite the wording, they didn't actually mean any quadrilateral. But what might they have meant, and what answers might be possible?

So here are some interesting questions:

• Under what circumstances is the answer one fifth?

• Is the answer always between a sixth and a fifth?
  • If not, what are the extreme values?

• Is every value in the range $[\frac{1}{6},\frac{1}{5}]$ achievable?

References

Here's the original tweet:

• https://twitter.com/MEImaths/status/774161733761966080

• http://www.ghira.mistral.co.uk/quadrilateral.ggb

<<<< Prev <<<< You Have To Admire Their Optimism

:

>>>> Next >>>> Surprisingly Quick ...

---

You should follow me on twitter

Comments

I've decided no longer to include comments directly via the Disqus (or any other) system. Instead, I'd be more than delighted to get emails from people who wish to make comments or engage in discussion. Comments will then be integrated into the page as and when they are appropriate.

If the number of emails/comments gets too large to handle then I might return to a semi-automated system. That's looking increasingly unlikely.