 Subscribe!
My lastest posts can be
found here:
Previous blog posts:
Additionally, some earlier writings:
|
Decision Trees in Games (Part 1) - 2011/05/15
A fairly standard exercise in probability is to ask who,
under a given scoring system, will win a game given the
probability of each move. For example, suppose we toss
a coin, and I get a point for every head, and you get a
point for every tail. Winner is first to 2.
It's easy if the coin is fair, because the game is
symmetrical. It's easy if it's a two headed coin, or a
two tailed coin, because then the winner is certain.
|
But if the coin shows head with probability p (and tail
with probability q=1-p) then it's harder. We need the
probability of 2 heads before 2 tails.
We can solve this by drawing a tree of what can happen.
We start at the top, and draw two arrows, one representing
a tail, the other for a head. From each of those places
we again draw two arrows, and so on. We stop when we've
got two heads, or two tails. The diagram at right shows
the result.
|
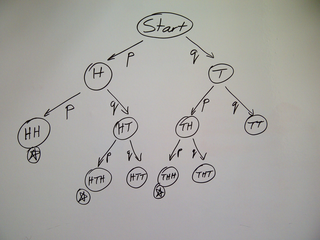
Decision tree for
"First to 2 heads"
|
|
We now have all the possibilities, and we can see that
there are three ways "H" can win: "HH", "HTH", "THH".
By tracing their respective paths down the tree we can
see the probability of each combination, and so we get
our answer of pp+pqp+qpp, which simplifies to
p2+2p2q
or
p2(1+2q).
We can check this in three particular cases. If the coin
is fair (so p=1/2 and q=1/2) then it should evaluate to
1/2. If it's a double headed coin (so p=1 and q=0) then
it should evaluate to 1, and if p=0 (so q=1) then it
should evaluate to 0.
And it does. That's nice.
|
This is fine for such a small problem, but it becomes
overly cumbersome if we wanted, say, first to 5, instead
of just first to 2. But then we realise: when the score
is 1:1 we don't care how we got there (although we do
care how many ways there were to get there). After "HT"
the score is 1:1, and after "TH" the score is again 1:1,
and so after that the possible options are all the same.
We can collapse the two states "HT" and "TH" into one
state, and just remember that there were two ways to get
there.
This is reflected in our answer. We have
p2
for the
straight line to the solution, but there are two ways of
going through 1:1, hence 2 lots of
p2q.
|
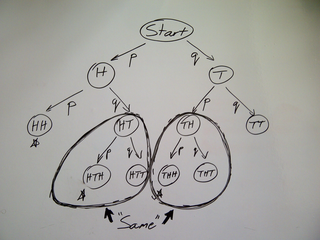
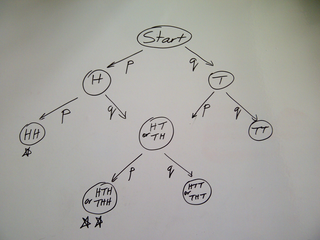
Merging identical sub-trees
|
|
For larger cases there are ways to do this algebraically
and without the diagrams, but personally, I find that
understanding and intuition comes from the diagrams, and
the counting arguments are guided by the structure in
the diagram, whether I draw the diagram, or simply think
of how to draw it.
|
So in larger cases we can collapse the tree into a more
compact structure, which in this case is a directed
acyclic graph (DAG) - "directed" because we have arrows
showing how we travel from score to score, and "acyclic"
because we never return to a previous score.
In a later post we'll look at non-cyclic structures, and
then find a surprise in an apparently well-understood game.
|
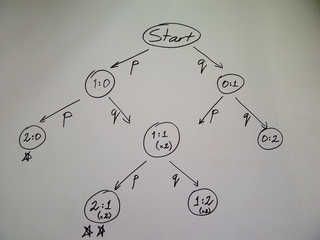
Decision DAG for
"First to 2 heads"
|
|
|
Suggest a change ( <--
What does this mean?) /
Send me email
