Elementary Estimates

Recent changes

Table of contents

Links to this page

FRONT PAGE / INDEX

Subscribe!

My latest posts can be found here:

Colins Blog

Previous blog posts:

Additionally, some earlier writings:

2019/01/08 - Elementary estimates

Introduction

Every now and again as I'm doing various estimates or calculations I use an approximation, and a few days ago it was brought home to me how much I rely on these, and how few people know them. So I thought I'd gather some of them together in one place to be a reference.

On the way I've attempted to give broad reasons as to why these are reasonable approximations, but each one can be explored in greater depth, and there are considerable subtleties in places. Even so, I hope these are interesting/useful.

By way of setting the scene, if $x$ is small compared to $1$, then $x^2$ is small compared to $x$. As a consequence, if $x$ is very small compared to $1$, $x^2$ is extremely small compared to $1$, and so we can get useful approximations in situations where $x^2$ is negligible. (My thanks to Rob Low[0] for this paragraph).

Getting started ...

The obvious question is: What exactly is "small enough"? I'm not going to answer that, it's a very deep rabbit hole ...
We start small by thinking about $(1+x)^2$. Expanding that we can see that $(1+x)^2 = 1 + 2x + x^2$, and when $x$ is small enough we can ignore the $x^2$ term.

So, roughly, when $x$ is small, $(1+x)^2\approx 1 + 2x$. We can see that with a little geometry, as follows.

Here we have a square of size $1+x$, where $x$ is smaller than $1$. We can see that the area of the entire square is made of of four regions, and these are of size $1$ for the big main square, $x^2$ for the little blue square, and $x$ for each of the two stripes, one at the top, the other on the side.

So the area $(1+x)^2$ is seen to be equal to $1+2x+x^2$.

But if $x$ is small enough the contribution of the little blue square is negligible, so we say that the area is roughly $1+2x$

And that's our result.

Now taking the square root of each side we can see that when $x$ is small, $\sqrt{1+2x}\approx 1 + x$, which we usually write as $\sqrt{1+x}\approx 1 + x/2$.

We'll use these a lot, and that will help you to remember them, but it's definitely worth keeping them close to hand.

When $x$ is small:

$(1+x)^2\approx 1 + 2x$
$\sqrt{1 + x}\approx 1 + x/2$

We'll use the approximation sign when we are
estimating or approximating, and an equals
sign when things really are equal. If you
find an incorrect usage, please let me know.
When working we often just use the equals
sign and sort it out afterwards, so there
could easily be errors.

Another thing to consider is $(1+x)(1-x) = 1-x^2$. When $x$ is small we can again ignore $x^2$, so $(1+x)(1-x) \approx 1$, which means that we have:

$\frac{1}{1+x} \approx 1-x$
$\frac{1}{1-x} \approx 1+x$

The second of these can be obtained
simply by taking $x$ to be negative.

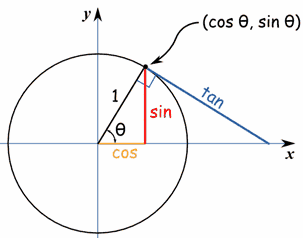
A tad of trig ...

Now let's look at distances in a circle. The basic definitions of $\sin(\theta)$, $\cos(\theta)$, and $\tan(\theta)$ are shown.

Some trig terms
The angles here aren't small, I know. This diagram is intended only to show the definitions of the different terms.

As the point on the circle moves down towards the $X$-axis you can see that the red line, "sin", gets closer and closer in length to the arc joining the $X$-axis to the point. Thus sin gets closer and closer to $\theta$ (when measured in radians).

We can see from the geometry that when $\theta$ is small, $\sin(\theta)$ and $\tan(\theta)$ are very close to $\theta$, and $\cos(\theta)$ is close to $1$. In fact, it's one of my standard mantras that for small $\theta$, $\cos(\theta)$ equals one. This is clearly not true, but in many circumstances it's close enough.

Remembering our Pythagoras, we can see from our "obvious" right-angled triangle that $\cos(\theta)^2 + \sin(\theta)^2 = 1$. But as we've said, when $\theta$ is small, $\sin(\theta)\approx\theta$. That means we can rearrange the above to get

$\cos(\theta) = \sqrt{ 1 - \sin(\theta)^2 }$

So:

$\cos(\theta) \approx \sqrt{ 1 - \theta^2 }$

Now recalling one of our approximations from the first section where we said, that when $x$ is small, $\sqrt{1+x} \approx 1+x/2$, we can now say that $\sqrt{1 - \theta^2}$ is roughly $1-\theta^2/2$.

So when $\theta$ is small, $\cos(\theta) \approx 1 - \theta^2/2$.

Going a step further

Since we have now got that $\cos(\theta) \approx 1 - \theta^2/2$, maybe we can extend our approximations a little more so they remain accurate even when $\theta$ or $x$ are a touch bigger. In particular, we observe that $(1+x)^3=1+3x+3x^2+x^3$. Certainly when $x^2$ can be ignored, $x^3$ will be even smaller, so we have:

$(1+x)^3 \approx 1 + 3x$.

But maybe $x$ is a tad larger, and $x^2$ can't be ignored, but $x^3$ is still small enough to ignore. Then we get the approximation:

$(1+x)^3 \approx 1 + 3x + 3x^2$.

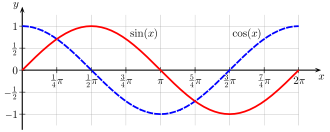
https://www.solipsys.co.uk/images/sin_cos.png

We can extend these ideas to see if we can improve the approximation for $\sin$ to values of $\theta$ that are a little larger.

If we look at the graph of $y=\sin(\theta)$, we can see that when $\theta$ is close to zero, the gradient is pretty much 1, which is the value of $\cos(\theta)$, and when $\theta$ is about $\pi/2$, the gradient goes from positive to negative, just as the graph of $\cos(\theta)$ does.

We can analyse this further and without too much work (but beyond the purpose and scope of this document) show that the slope (or gradient) of the graph $y = \sin(\theta)$ is the value of $\cos(\theta)$. In other words, $\frac{d}{d\theta}\sin(\theta) = \cos(\theta)$.

I'm still working on finding a way to derive this without using calculus, but instead just with a little algebra, geometry, or both in combination. I'd welcome any thoughts or suggestions on that.
Update: got one! I won't put it here, but I'll write it up in a separate post/page.
Well, $\cos(\theta) \approx 1 - \theta^2/2$, so we can integrate that to get $\sin(\theta)$, and that gives us our next approximation:

$\sin(\theta) \approx \theta - \theta^3/6$

This is still only true for small values of $\theta$, (again, whatever that means) but in a sense it is "more true" than the first approximation that we had.

Now for the Tangent Function

Time now to turn our attention to $\tan(\theta)$.

When $\theta$ is really small we can see from our diagram that $\tan(\theta)\approx\theta$. We can also see that by recalling that $\tan(\theta)=\sin(\theta)/\cos(\theta)$, and that $\sin(\theta)\approx\theta$ and $\cos(\theta)\approx 1$. But we can go a step further with our more accurate approximations for $\sin$ and $\cos$.

Since $\cos(\theta)\approx 1-\theta^2/2$ we also have $1/\cos(\theta)\approx 1+\theta^2/2$.

So $\tan(\theta) \approx ( \theta - \theta^3/6 )( 1 + \theta^2/2 )$ which expands to: