Subscribe!

• Colins Blog

• Rage Inducing System Implementation
• The Book Is Not Always Right
• Emerging E
• Impossible To Translate
• Waiting In Vain
• Non Repeating Decimals
• Rational Repeats
• Why Is It Lovely
• Compiling Crypto Connections
• Exploring Connections Between Crypto Systems
• Elwyn Berlekamp Has Left Us
• Root Cause Analysis And The Photocopier Question
• The Up Down Tides
• The Fore Aft Tide
• The Sideways Tide
• Wrapping Up Wrapping Up The Earth
• The Other Wrapping The Earth Problem
• Wrapping The Earth
• The Ring Of Steel
• Rounding Up The Ropes
• Other Other Other Rope Around The Earth
• Rope Around The Earth Refined
• The Other Rope Around The Earth
• Elementary Estimates
• Latitude Correction
• Just Give Me The Answer
• More Musing On Pollard Rho
• Idle Thoughts About Pollard Rho
• When Optimising Code Measure
• A Dog Called Mixture
• Another Pay Pal Scam
• Why Top Posting Has Won
• Unexpected Interaction Of Features
• Archimedes Hat Box Theorem
• Considering A Sphere
• To Link Or Not To Link
• Generic Advice For Writing A Thesis
• Just Teach My Child The Maths
• Not A Spectator Sport
• Left Truncatable Prime
• The Doctor And The Lawyer
• Four Points Two Distances Proof
• Meeting Ron Graham
• Napkin Ring Versus Spherical Cap
• The Four Points Puzzle
• Radius Of The Earth Part Two
• Grep Timing Anomaly
• The Radius Of The Earth
• This Works To Cure My Hiccoughs
• Perhaps We Saved One
• Thinking About Mastodon
• Disappearing Trains On Virgin
• The Independence Game
• One Of My Favourite Puzzles
• Thinking About Recursion
• Memorising The Tube
• Spikey Spheres
• Surprisingly Quick
• An Unexpected Fraction
• You Have To Admire Their Optimism
• Representatives Matter
• Pythagoras By Incircle
• A Puzzle About Puzzles
• How Not To Do Twitter
• Calculating 52 Factorial By Hand
• Small Things Might Not Be So Small
• Not If You Hurry
• Factoring Via Graph Three Colouring
• Another Proof Of The Doodle Theorem
• When Obvious Is Not Obvious
• Graph Three Colouring
• The Doodle Theorem
• Be Careful What You Say
• The Mutilated Chessboard Revisited
• A Mirror Copied
• The Other Other Rope Around The Earth
• Photocopy A Mirror
• The Point Of The Banach Tarski Theorem
• Sieve Of Eratosthenes In Python
• Fast Perrin Test
• Russian Peasant Multiplication
• FindingPerrinPseudoPrimes Part2
• FindingPerrinPseudoPrimes Part1
• The Unwise Update
• Miles Per Gallon
• Tracking An Item On Hacker News
• Hacker News User Ages
• Poking The Dusty Corners
• There Is No Time For This
• Publically Sharing Links
• Learning Times Tables
• Graceful Degradation
• Diagramming Maths Topics
• On The Rack
• Square Root By Long Division
• Beyond The Boundary
• Fill In The Gaps
• Software Checklist
• NASA Space Crews
• The Birthday Paradox
• The Trapezium Conundrum
• Revisiting The Ant
• The Ant And The Rubber Band
• Irrationals Exist
• Multiple Choice Probability Puzzle
• Random Eratosthenes
• Wrapping Up Square Dissection
• Dissecting A Square Part 2
• Dissecting A Circle
• Dissecting A Square
• An Oddity In Tennis
• Decision Tree For Tennis
• Decision Trees In Games
• A Matter Of Convention
• Do You Nourish Or Tarnish
• Binary Search Reconsidered
• Two Equals Four
• The Lost Property Office
• The Forgiving User Interface
• Setting Up RSS
• Withdrawing From Hacker News

• Random Writings.
• Colins Blog 2010
• Colins Blog 2009
• Colins Blog 2008
• Colins Blog 2007
• Colins Blog Before 2007

As an experiment, we can punch "10" into a calculator and take the square root. Given that we're starting with a number that's bigger than 1, it's no real surprise that we get a smaller number. In fact, we get 3.16227766...

We can take the square root of that, and we get 1.77827941...

Now, if you actively like numbers, you may think that that is quite close to one and seven ninths, or $1\frac{7}{9}$. If we write that as an "improper fraction" it's $16/9$. And the fun thing about $16/9$ is that both $16$ and $9$ are squares, so if we take the square root again we should get something very close to $4/3$.

And we do - we get 1.333521432...

Winding this backwards, and squaring up $4/3$ multiple times, we can see why this happens. Taking $\left(\frac{4}{3}\right)^8$ we get $65536/6561$, which is very close to 10.

We can continue the process to see if anything new and interesting happens, and it's not too long before our numbers are basically one plus a little bit of small rubbish.

$n$ $p=2^n$ $10^{1/p}$ $c$ 0 1 $10^{1/1}$ 10.00000... 1 2 $10^{1/2}$ 3.162278... 2 4 $10^{1/4}$ 1.778279... 3 8 $10^{1/8}$ 1.333521... 4 16 $10^{1/16}$ 1.154782... 5 32 $10^{1/32}$ 1.074608... 6 64 $10^{1/64}$ 1.036633... 7 128 $10^{1/128}$ 1.018152... 8 256 $10^{1/256}$ 1.009035... 9 512 $10^{1/512}$ 1.004507... 10 1024 $10^{1/1024}$ 1.002251...

A quick note - using the laws of exponents, taking the square root of a number is raising it to the power of $1/2$. Doing this again is multiplying the exponent by half again. So the square root of the square root is $x$ to the power of $\frac{1}{2} \times \frac{1}{2}$, which is $\frac{1}{4}$. And so on. If you're not familiar with this then you don't need to know it, you can just take my word for it and read on, but if you want to know more then either let me know and I'll write a summary page, or check on the web.

So, if we plot the result against how many times we've taken a square root it looks like this:

Ignoring the first few terms we get this:

So as we take more and more square roots we end up with one plus some small rubbish, but looking at the small rubbish we can see something interesting. Compare the lines for 9 and 10. On line 9 the power is $1/512$, and the rubbish is $0.004507...$. On line 10 the power is $1/1024$, and the rubbish is $0.002251...$. The power halves because we're taking the square root, fine, but the rubbish also halves, and that is cause for pause.

$x$ $10^x$ 0.0110 1.0253 0.0100 1.0233 0.0090 1.0209 0.0080 1.0186 0.0070 1.0162 0.0060 1.0139 0.0050 1.0116 0.0040 1.0093 0.0030 1.0069 0.0020 1.0046 0.0010 1.0023 0.0000 1.0000

So when the power is already small, halving the power, halves the rubbish.

That's interesting. To have a closer look at this we can generate a table of the rubbish when we have small powers. So for a small power of $x$ we plot compute $10^x$. The table is shown here at left, and we can see, as expected, we're getting one plus small rubbish. Now let's subtract off the one and see what we've got. Best seen in a plot:

It's a straight line! Well, nearly a straight line. So it looks like when the power is small, when $x$ is small, the value of $10^x$ is 1 plus rubbish, where the rubbish is a multiple of the power. So when $x$ is small, there is a constant $c$ such that:

So the process of taking repeated square roots, looking at the rubbish, and comparing with the power, has given us a constant, and in this case if we measure the constant we get an answer of around 2.302585...

But I say "in this case" because we started with 10, and we can wonder whether we get a different answer if we start with, say, 5 instead. So we can go through the process again, this time starting with 5, and we end up again with a straight line graph, but the slope is different! This time the slope is about 1.6094379...

Start Constant 10 2.302585... 5 1.6094379...

So if we start with 10 we get 2.302585... and if we start with 5 we get 1.6094379... and we can start a chart, shown here at right.

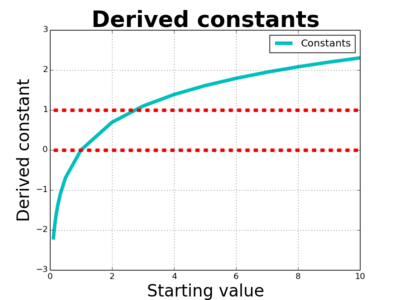
So how can we fill in more values?

Well, given a starting value $S$, we're asking for a constant, $c$, such that when $x$ is really small, the value of $S^x$ is roughly $1+cx$. Here is a plot of the rubbish for starting values of 2, 3, 5, and 10:

So for each starting value we want to compute the constant. To do so - at least approximately - we pick some small number $x$ to use as a power, something like one millionth. Then for each starting number, $S$, we compute $\frac{1}{x}(S^x-1)$. We've got the first couple of values, and now we can fill them in:

Start Constant 2 0.693147 3 1.098613 4 1.386295 5 1.609439 6 1.791761 7 1.945912 8 2.079444 9 2.197227 10 2.302588

There are a couple of things to notice - the numbers are not just random - we can find connections between them. For example, look at the constants for 2, 5, and 10. We can add the constants for 2 and 5 and we get 0.693147 + 1.609439 = 2.302586, which is close to the constant for 10. That's particularly interesting, because 2 times 5 is 10. Have a look at the constants for 2, 3, and 6, and you'll find the same thing happens.

So if X times Y equals Z, maybe, just maybe, the constants for X and Y add to give the constant for Z.

Why would that be?

But that's not the direction I'm going. Instead, notice that the constants are growing:

I've included starting with some values less than one, as well as the value for one itself, and now we can see some clear features.

Some people may scoff and say "Well obviously there's a value that gives an answer of 1 - it's completely obvious from the plot you've shown." Well, if you square the fraction $\frac{7}{5}$ you get an answer that's just below 2, and as you increase the fractions being squared, you end up above 2, so "obviously" there is a fraction that when squared gives exactly 2. Except that that turns out not to be the case. There is no fraction which when squared gives exactly 2, so some care is warranted.

Firstly, when $x$ is 1, the derived constant is exactly 0. We'll leave that as an exercise for the (mythical) interested reader. Another other point of interest is that it starts below the value of one, and then goes above the value of one, so maybe, just maybe, there is a starting value $S$ that results in a constant of exactly 1.

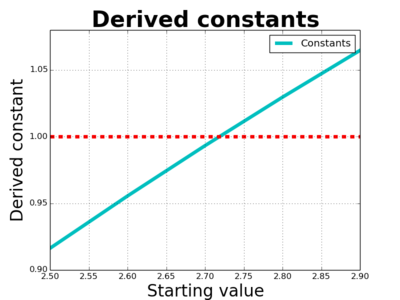
So we can explore this question. Let $x$ be really small, and find a value $S$ such that $\frac{1}{x}(S^x-1)$ is equal to 1. Can we do that?

So let's plot between 2.5 and 3.0:

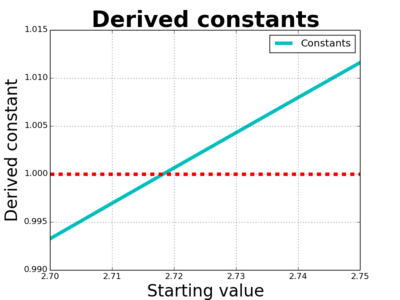
OK, so it's between 2.70 and 2.75 - let's look at that in more detail:

We can now see that it's just a bit less than 2.72 or thereabouts.

Some of my readers will have been shouting at the screen for some time now - "It's $e$!! It's $e$!!" Well, yes, it's $e$, also known as Euler's number (Note: not Euler's constant, that's something different).

Tracking back through our derivation here, we are trying to solve this problem/question:

• Find a value $v$ such that $$\lim_{x\rightarrow 0}\frac{1}{x}(v^x-1) = 1$$.

<<<< Prev <<<< Rage Inducing System Implementation

:

>>>> Next >>>> Powers Of Two In Lex Order ...

---

You can follow me on Mathstodon. Of course, you can also follow me on twitter:

---

Send us a comment ...

You can send us a message here. It doesn't get published, it just sends us an email, and is an easy way to ask any questions, or make any comments, without having to send a separate email. So just fill in the boxes and then

Your name	:
Email	:
Message	: