Four Points Two Distances Proof

Recent changes

Table of contents

Links to this page

FRONT PAGE / INDEX

Subscribe!

My latest posts can be found here:

Colins Blog

Previous blog posts:

Additionally, some earlier writings:

2017/10/03 - Four points - the proof

This page has been
Tagged As Maths.
The Four Points Puzzle challenge that Peter Winkler set me was this:

Find all configurations of four (distinct) points in the plane that determine exactly two distances.

As I remarked earlier, given four points there are six possible pairs, so in general, four points in the plane will determine six distances. But we can choose to place the points to create duplication, and the challenge here is to find all possible ways to do that and end up with only two distances.

That's reasonable, and lots of people have sent me their solutions. Peter had also said:

"Nearly everyone misses at least one, and for each possible solution, it's been missed by at least one person."

So the challenge isn't really to find all the configurations so much as to be able to prove that you have them all. That's what I'm going to do here, so if you haven't had a go at the puzzle, now is the time to bookmark the page, close the browser, get yourself a tea, coffee, or other beverage of your choice, and have a go.

Remember, it's the proof that matters.

Here's mine.

Preliminaries ...

We have four points, and therefore six pairs. But we only have two distances, so some are short, and some are long. The short ones are all the same as each other, and the long ones are all the same as each other. Obvious, I know, but we're just warming up.

So let's prove a few simple results.

Lemma: No three points are collinear.

(If you're happy with this you can skip the box)

These sorts of proofs, descriptions, and discussions can really stretch your visualisation skills. If you're an experienced mathematician you'll know that you can't just skim this sort of thing and try to "Read like a novel" - you need to take pencil/pen and paper and draw what's going on. And if not literally with pen and paper, then at least to work on explicitly visualising it.
You need to "Read like maths" - because it is.
If points $A$, $B$, and $C$ are collinear, with $B$ between $A$ and $C$, Then $|AC|$ is the long distance, and both $|AB|$ and $|BC|$ are the short distance. Consider point $D$ ... we have two possibilities.
If $D$ is the same distance from $A$ and $C$ then that must be the long distance, but then $|BD|$ is neither $|AB|$ nor $|AC|$. So that doesn't work.
So $|AD|$ and $|CD|$ are different lengths. Up to symmetry we can compute exactly where $D$ must lie, then observe that again, $|BD|$ is neither of our possible lengths, so that doesn't work either.
So there is nowhere to put point $D$, and hence no three points can be collinear.

Observation: Each edge is in exactly two triangles. (It's worth taking some time to convince yourself of this)

Lemma: There are at least two short edges that share a vertex.

(Again, if you're happy with this, skip the box)

We cannot have no short edges, because then we'd have all long edges, and the points would have to be in a tetrahedron, which isn't in a plane.
We cannot have exactly one short edge, because then the other five would all be long, and have to form two equilateral triangles with a shared edge. The remaining edge would have to be longer.
So we must have two or more short edges. Any three or more edges must share at least one vertex, so we only need to worry about the case where we have exactly two short edges.
We cannot have $|AB|$ and $|CD|$ as the only short edges, because both $C$ and $D$ would have to be on the perpendicular bisector of the line $AB$, and they would have to be on opposite sides of the line, making $|CD|$ too long. So if there are exactly two short edges they must share a vertex, which is what we need.
So there are (at least) two short edges that share a vertex.

Now for the single insight that, I think, makes the enumeration of all solutions quite straight-forward. The fact is simple, making certain it is a fact is a little tedious - feel free to skip this section if you're happy with the statement of the lemma.

Lemma: There is a triangle with two short and one long side.

We proceed by the cases of how many long edges there are.

We cannot have no long edges.

If there is exactly one long edge then either triangle it forms will suffice.

If there are exactly two long edges, consider one of them. It is part of exactly two triangles, at most one of which can contain the other long edge, so at least one of which has two short sides.

If there are exactly three long edges then we have three short edges. Take two that share a vertex - $AB$ and $BC$. If $AC$ is short then all distances to $D$ would have to be long, which is not possible. So $AC$ is long, and $ABC$ is our required triangle.

If there are exactly four long edges then the two short edges share a vertex and the remaining edge of that implied triangle is long.

We cannot have exactly five or six long edges.

So we are done.

Finding all solutions ...

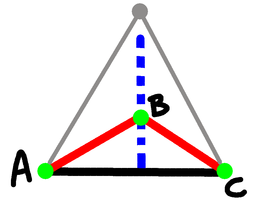
Triangle with
two short sides
So now we know that there is at least one triangle with two short sides and a long side. So let's call that $ABC$ with $AC$ being the long edge. We can see that $B$ has to be on that blue line, above the line $AC$, and because the red lines are the shorter ones, $B$ cannot be as high as the grey point, which forms the equilateral triangle with $A$ and $C$.

Now let's consider the fourth point, $D$. We can assume that $D$ is on or to the right of the blue line, because if it isn't, reflect around that line, and now it is!

The distances from $D$ to each of $A$, $B$, and $C$ must be short or long, so let's write all the possible combinations of each of those distances.

Case	Distance to $A$	Distance to $B$	Distance to $C$
0	Short	Short	Short
1	Short	Short	Long
2	Short	Long	Short
3	Short	Long	Long
4	Long	Short	Short
5	Long	Short	Long
6	Long	Long	Short
7	Long	Long	Long

Cases 1 and 3 are not possible, for then $D$ would be to the left of the blue line, which we have excluded.

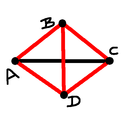
Case 0 (sss): Point $D$ has to be the reflection of point $B$ across the line $AC$ giving a pair of equilateral triangles that share an edge.

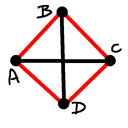
Case 2 (sls): As case 0, point $D$ has to be the reflection of point $B$ across the line $AC$. In this case we get a square with $AC$ and $BD$ as diagonals.

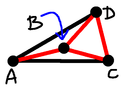
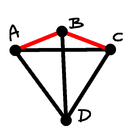
Case 4 (lss): The triangle $BCD$ is equilateral, and $ACD$ is isosceles.

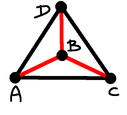
Case 5 (lsl): Here $ACD$ is equilateral, and $B$ is in the middle. Point $D$ must be where the grey point is on the diagram above.

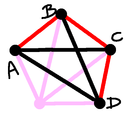
Case 6 (lls): Here $D$ is a little below $C$, and the four points are the points of a regular pentagon.

Case 7 (lll): Now point $D$ forms an equilateral triangle with $A$ and $C$, and must be the opposite side of the line $AC$ from the point $B$. The points form a kite.

So there are 8 combinations, two of which are impossible, and the other six give exactly one solution. The only remaining question is whether any of the options might give more than one possible solution, but that doesn't happen. In each case the location of point $D$ is completely determined by the options given, so we're OK.

And we are done.