In Defense Of The Axiom Of Choice

Recent changes

Table of contents

Links to this page

FRONT PAGE / INDEX

Subscribe!

My latest posts can be found here:

Colins Blog

Previous blog posts:

Additionally, some earlier writings:

This page has been
Tagged As Maths

The first of a two-parter, here we provide a reason to accept that the Axiom Of Choice is reasonable, and should be used.

The back-story is a long one, and I won't go into it here. This is intended just as a bit of an overview so you can go and read more if you're interested. But in essence, the naïve set theory that Georg Cantor came up with was found to have a paradox. In Cantor's set theory, a set was simply a collection of things, and a new set could be defined by saying:

This set contains all things that satisfy property P.

Then Bertrand Russell said:

Let R be the set of all sets that do not contain themselves.

That's a problem, because if R is in R then R cannot be in R, and if R is not in R then it satisfies the condition, and hence must, after all, be in R.

That's a problem, so to put set theory on a firm footing, axioms were devised.

Enter Ernst Zermelo and Abraham Fraenkel

To do this, Ernst Zermelo and Abraham Fraenkel came up with axioms to formalise set theory. There are many different collections of axioms that are all equivalent to each other, and these collections have been studied extensively. But there is one axiom that people still argue about, and that's the Axiom Of Choice.

So what's that?

Let's talk about the product of sets.

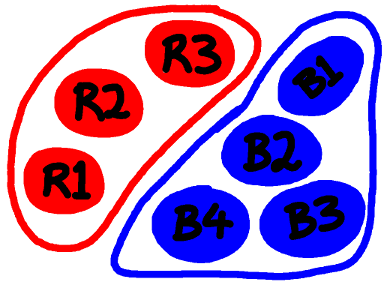
Taking pairs.

Loosely, a set is a collection of things. To start with let's have a set R with three red things, and a set B with four blue things.

https://www.solipsys.co.uk/images/ThreeRedFourBlue.png

Suppose now I want to take one red thing and one blue thing and put them in a bucket. How many ways can I do this? Here's the list:

$R_1, B_1$	$R_1, B_2$	$R_1, B_3$	$R_1, B_4$
$R_2, B_1$	$R_2, B_2$	$R_2, B_3$	$R_2, B_4$
$R_3, B_1$	$R_3, B_2$	$R_3, B_3$	$R_3, B_4$

There are twelve, because there are 3 choice of red thing and four choices of blue thing, and the product of 3 and 4 is 12.

And that happens every time we choose a pair of things, one from each of two finite sets. The size of the collection of possible pairs is the product of the sizes of the two sets from which we are choosing.

By analogy, we say the product of sets A and B is the collection of pairs.

A nice thing happens here. Given three finite sets, A, B, and C, we can define the triple product as being the collection of triples, and again, the size of AxBxC is the product of the sizes of A, B, and C. We can also see that there are matchings between (AxB)xC, AxBxC, and Ax(BxC). So while we don't quite get associativity, we certainly get something very like it.

So we can define the product of a finite collection of finite sets, and it all feels quite natural.

What about infinite collections of infinite sets?

There seems to be no reason to limit ourselves to finite sets. If A and B are infinite we can still construct the collection of pairs, the first from A and the second from B. We can't talk about the product of the sizes in the same way as we can with finite sets, but it seems to make sense.

We need to be a bit careful here, because sets can't contain repeated elements, but that doesn't really cause any problems. So here is the situation:

Suppose we have a collection of sets that are:
- (a) non-empty, and
- (b) disjoint
  - (so no element appears in more than one set)

Then the product of these sets is all the ways we can choose exactly one from each.

Seems reasonable ... yes?

The Axiom Of Choice

We can show that using the axioms of Zermelo-Fraenkel Set Theory we cannot prove the product of an infinite collection of non-empty sets to be non-empty. That seems daft, so it makes sense to add that as an axiom.

The Axiom Of Choice states that the product of non-empty sets is always non-empty.

For a finite collection of finite sets this is an absolute no-brainer, we can (as we did earlier) literally list all of the elements of the product. It seems perfectly reasonable to say that the product of non-empty sets is always non-empty.

Thus we have the case for the Axiom Of Choice.

Next time we'll look at the case against.