Infinite Ramsey Theorem

Recent changes

Table of contents

Links to this page

FRONT PAGE / INDEX

Subscribe!

My latest posts can be found here:

Colins Blog

Previous blog posts:

Additionally, some earlier writings:

With the passing of Ron Graham a few people have been in touch with me to ask what "Ramsey Theory" is. So I've given a brief outline, and pointers in case people want to follow up. In truth, just stick "Ramsey Theory" into your favourite search engine and you'll get lots to follow up and chase down (as opposed, of course, to "follow down" or "chase up").

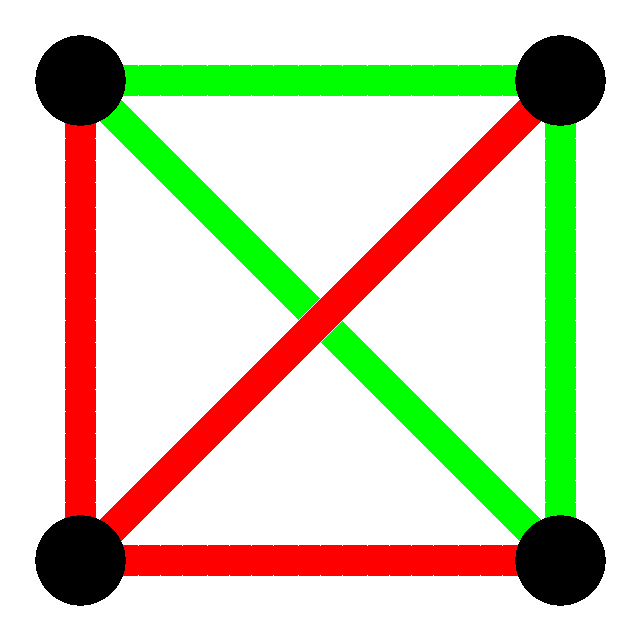
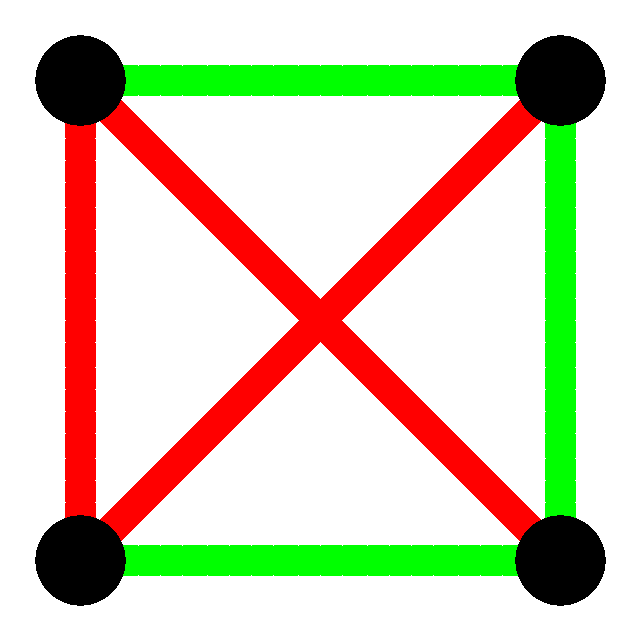
So here I'll try to give a little context, and an actual proof.

The basic idea is that "absolute disorder is impossible", a statement that clearly requires refinement and clarification. So here is the starting place, and some motivation.

Suppose you have four points, and join each to all the others, giving six lines in all. We don't care if the lines cross, we actually only care about the joining of the dots. This is an example of a "Graph" as in "Graph Theory", some people call it "Network Theory", and say this is an example of a "Network". The exact terms don't matter.

So we have four points (or vertices, or nodes) each joined to all the others. The connectivity is complete, and in Graph Theory this is called the complete graph on four vertices, or $K_4$.

Now we colour the lines, each one being either red or green. If they are all the same colour then the graph is "mono-chromatic". (not very original or inventive, but you don't want everything to be weird and unguessable). Here are two examples:

To be explicit, $K_3$ is the complete graph on three points. You can think of it as a triangle.

The examples here both have exactly three green lines and exactly three red lines ... that doesn't have to be the case. In general, we can have any number of either.

Notice that the one on the left has three points that are all connected only by green lines. There is, hiding in this graph, a mono-chromatic (in this case green) $K_3$. This isn't always the case, as you can see from the graph on the right. Remember, we only care about the lines going from point to point, and there isn't a point in the middle, so the "sort of triangle" in red doesn't count (and if you never even noticed it ... good!)

OK, so when we have four points and colour all the lines between them either red or green, we may or may not have a monochromatic triangle.

What about with five points? With a little work we can show that the same is true ... there might be a monochromatic triangle, or there might not be, it's all down to the colouring.

What about with six points?

I won't prove that here. If you're interested you can try for yourself to see why it's true, you can look it up on t'internet, or you can ask me via the comment box (or email). I'd be happy to explain, or to point you at a proof.
That's where it changes. With six points, no matter how hard you try, every colouring of all the lines, using two colours, will result in a monochromatic $K_3$ somewhere. There will always be either a red $K_3$, or a green $K_3$.

This is often made into a little story, with 6 people at a party, and the claim is made that you can either find three who have all mutually shaken hands, or three who have not (or both). Or you can find three who are all "friends" on Facebook, or three who are not, or both. And so on.

But that makes it harder to generalise later, so it's perhaps best to stick with the more abstract version.

Well, let's be more general. Bear with me for a bit, or skip over this bit and come back to it later.

What if we want not just a monochromatic $K_3$, but a monochromatic $K_4$
- Is there always a point where that is inevitable?
  - Yes.
What if we say we want either a green $K_5$ or a red $K_9$
- Does that become inevitable?
  - Yes.
What if we say we want either a green $K_{37}$ or a red $K_{23}$
- Does that become inevitable?
  - Yes.

And so on.

So Ramsey's Theorem, in particular, Ramsey's finite Theorem, says that for any positive integers $g$ and $r$, there is always a size, $n$, where in a red/green edge-coloured $K_n$ there will be either a red $K_r$, a green $K_g$, or both. This number is called $R(g,r)$, while it's true that it always exists, and it's always finite, we don't actually know most of the values. Paul Erdos related the following anecdote:

"Aliens invade the earth and threaten to obliterate it in a year's time unless human beings can find the Ramsey number for red five and blue five [that is, $R(5,5)$]. We could marshal the world's best minds and fastest computers, and within a year we could probably calculate the value. If the aliens demanded the Ramsey number for red six and blue six, however, we would have no choice but to launch a preemptive attack."

And yet, even though we know almost nothing about the finite cases, we do know something about the infinite case.

The Infinite Ramsey Theorem

So let's think about all the positive integers, and think about joining every pair with a line. So 1 is joined to 2, 3, ... 13, 14, 15, ... 23, 24, ... well, you get the idea. Likewise 2 is joined to 3, 4, 5, ..., 17, 18, 19, and well, everything. So every pair of positive integers is joined by a line.

We can think of this as $K_\infty$.

And let's colour each line either red or green. Or better yet, have someone else do it.

The problem with having someone else do it is that you don't know what they've done. But Ramsey's Infinite Theorem says this:

Theorem

No matter how we two-colour the edges in $K_\infty$, it will always be possible to find infinitely many points that are all connected by the same colour.

In other words, we will always be able to find a monochromatic $K_\infty$ within.

And now I'll show you the proof.

Proof

Let's look at the first part of the graph we have:

This is harder to explain in words than it is to simply do "by hand" for yourself. Don't just read this, get some paper and think about carrying out the procedure for yourself, for real.
Call this Point A.
It's a mess, so let's just start with the first vertex/point/node. It's connected to everything, so going to the right are infinitely many lines, each either red or green. Let's for the moment assume there are infinitely many green lines going off to the right from that node. Then what we do is colour that node green, and then delete every node that is connected to it with a red line.

Got that? If there are infinitely many green lines from this node going rightwards, we look at all the red lines from this node, and delete the destinations. We also colour this node green to remember we've done it.

But what if there are not infinitely many green lines going to the right? Then there must be infinitely many red lines going to the right, so we colour this node red, and delete all the rightwards nodes connected to it with a green line.

Hang on to that ... come back and re-read in a moment.

Now the original second node might have been deleted, but we know we still have infinitely many nodes remaining, so we move on to the next one, and look at the lines going right-wards from it. We do as we did last time. If there are infinitely many greens going to the right then we keep them, delete everything hit by a red line going to the right from this node, and colour this node green. Otherwise we colour this node red, and delete all the ones connected (to the right) with a green line.

This might be a good time to go back to Point A and re-read the section. Only a few times, obviously.
Again, we are guaranteed to keep infinitely many nodes, and now all the lines going rightwards are the same colour, be it red or green.

Here's a diagram:

So what?

Now we have infinitely many points, and for each of them, all the lines going to the right are the same colour. How many green points do we have?

If we have infinitely many green points then we keep them, discard the others, and now we have infinitely many points with all the lines going to the right coloured green. But that means all the lines are coloured green, and we have accomplished our goal. We have found an infinite collection of points such that all interconnecting lines are the same colour.

But what if we only have finitely many green points? Well, in that case we must have infinitely many red points, and the same thing applies!

So in either case we can find infinitely many points with all lines between them coloured the same, and that completes the proof.

Generalisations ...

So there are a few things we can do now. What about more than two colours? Can we prove the finite Ramsey Theorem from the Infinite Ramsey Theorem? What about sub-structures other than monochromatic complete graphs? And so on.

Ramsey Theory is deep, rich, and this is just a taster for the sort of questions asked. In particular, we can go back to Ron Graham and look at a specific question he was working on:

Yes, it does make sense to talk of a $D$-Dimensional cube. Honest.

Take the vertices of a $D$-Dimensional cube, and bi-colour all the edges connecting all the vertices, including the "diagonals", and not just the edges of the cube. So we have $2^D$ vertices, and every pair of them is connected with an edge. We can ask:

Is there a monochromatic $K_4$ with all the points in a plane?

The answer is that once $D$ is big enough then yes, you can always find a planar $K_4$. How big? That's where it gets interesting.

Graham proved that it worked once $D$ was a particular size, but the size was so big he had to invent a special notation for it. If every atom in the universe was turned into ink there still wouldn't be enough to write the number, not to mention that there would be neither paper, nor someone to do the writing!

The number is now known as "Graham's Number", and for a time it was the largest number ever used in a mathematical proof.

The real number is known to be bigger than 13.