More Musing On Pollard Rho

Recent changes

Table of contents

Links to this page

FRONT PAGE / INDEX

Subscribe!

My latest posts can be found here:

Colins Blog

Previous blog posts:

Additionally, some earlier writings:

More thoughts about Pollard Rho

The previous post can be found here:

Idle Thoughts About Pollard Rho

This page has been
Tagged As Maths
After my previous post I started to explore a little more about how the function in Pollard Rho affects what's going on. As yet I've not come to any conclusions, and I'm currently deep in the "I'm confused" stage of the exploration. I'm sure there are other people know all this, but I don't know who they are, and haven't been able to find any write-ups, so I'll just carry on.

The role of the function ...

Pollard Rho works by iterating a function $f:Z_n -> Z_n$ and we look for a cycle modulo $p,$ where $p$ is a factor of $n$. The usual function is $f(x)=x^2+c$ for some $c$, and I was wondering about using another function that "hops about" pseudo-randomly, and whether that would work. But my first attempt didn't seem to work, and I speculated that the quadratic nature might actually matter. The quadratic form means that nodes in the transition graph all have out degree 1, but in degree either 0 or 2. Maybe that matters.

So I decided to experiment with random graphs of different in-degrees.

Having in-degree $k$ ...

#!/usr/bin/python import sys from random import * n = int(sys.argv[1]) k = int(sys.argv[2]) nodes = range(n) targets = sample( nodes, (n+k-1)/k ) targets = k*targets shuffle(targets) for node in nodes: print targets[node]

This Python program takes a value $n$, which is the number we think we want to factor, and an in-degree $k$ for the graph nodes. We randomly select $n/k$ elements from the range $0$ to $n-1$, and then replicate those elements $k$ times, and shuffle them. The result is a list which for each element shows who it gets mapped to. Every element either has nothing coming in, or $k$ coming in.

So we pick a value of $n$ - say $n=10000153$ - and then for each $k$ in the range $1$ to $4$ we generate the graph. Having done so, we then run the Pollard Rho algorithm.

What happens when we factor?

mapping = [ int(x.strip()) \ for x in \ file(sys.argv[1]).readlines() \ ] n = len(mapping) k = int(sys.argv[2]) rabbit, turtle, steps = k, k, 0 while True: rabbit = mapping[mapping[rabbit]] turtle = mapping[turtle] steps += 1 if gcd(rabbit-turtle,n) != 1: print gcd(rabbit-turtle,n), steps sys.exit(0)

Having produced random "functions" we can now use the Pollard Rho factoring algorithm to try to factor the number we started with. In doing so, we can see if the in-degree seems to have an influence on how quickly we factor. It's not really the "time" that matters, it is the number of "steps" we take in the factorisation.

The hope is that with larger in-degrees the graph will be more "squat" and we'll home into a cycle more quickly. That would mean that we take fewer steps, so it will run more quickly. We're still not looking at a huge improvement, but who knows.

So let's run this, and give several different possible starting nodes to try to see if we get some sort of spread.

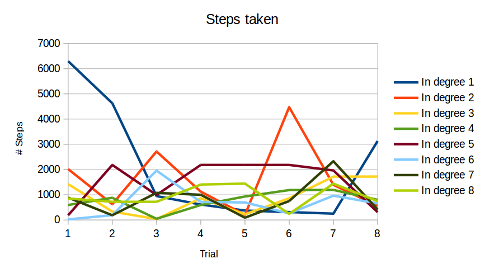https://www.solipsys.co.uk/images/PollardRhoTiming.png

Well, that's disappointing. There doesn't actually seem to be any real change, even though you'd hope that with an in-degree of 4, or 8, perhaps you'd zoom in on the cycle more quickly. But these experiments appear not to support that.

Of course I'm still using relatively small numbers, about $10^7$, so maybe that matters. But even so ...

I guess I really don't understand this.

<<<< Prev <<<<

Idle Thoughts About Pollard Rho

>>>> Next >>>>

Just Give Me The Answer ...