P Vs NP

One of the Millennium Problems is to determine whether the complexity class P is the same as the complexity class NP, or whether they are different.

In essence, this question is asking whether some calculations that are intrinsically hard (for some technical definition of "hard"), or whether all problems are effectively easy (for some technical definition of "easy".) The Knapsack Problem, for example, is thought to be hard, but no one really knows for sure. It may just be that no one has yet been clever enough to find the "right" way to do it.

The basic ideas

Before we can discuss how hard a problem might be, we have to be very precise about what a problem really is. What does it mean to talk about "a problem"? What is "a problem"?

In the context of complexity theory, a "problem" is a collection ( invariably infinite in size) of questions. Each question is called an "instance" of the problem. We can talk about the "size" of the question, and then we can talk about how long it takes to solve questions of different sizes.

To avoid unnecessary complexity here, and to keep this overview simple, we will give three examples of problems, and discuss the definitions in relation to them. The three example problems are:

Multiplication
- Example questions:
  - What is 5 * 13 ?
  - What is 21966 * 58433 ?
  - What is 83091794910922588011 * 53157592291179325404 ?
Factoring
- Example questions:
  - What are the factors of 187 ?
  - What are the factors of 10411 ?
  - What are the factors of 176622777566231251 ?
Graph colouring
- Example questions:
  - If I give you a list of people and which of them are friends, how can we assign them to jobs so that no friends are on the same job (so they don't slack off)?
    - For example: people = [A,B,C,D], three jobs, and friends = [AB,BC,AC,AD]. One solution is jobs = [ [A], [B], [C,D] ].
    - (My thanks to an unknown contributor)

For a given problem, and therefore a given collection of questions, it takes a certain number of symbols to say which question we're interested in. In general, some questions are bigger - as seen from the examples given above. We can expect that larger questions will take longer to answer.

The question is - how long?

Time complexity of an algorithm

For a given algorithm we can give limits on the time it takes to run, and this limit is usually given as a function of the size of the problem.

Take multiplication. The "long-multiplication" that used to be taught in school takes a very specific number of operations. If the first number has a digits, and the second number has b digits, then in general the act of multiplying them (using that method) requires a*b (and a bit) "actions".

If the numbers being multiplied are about the same size, then the formula becomes simpler. In general we ignore the smaller terms, and the constant at the front, and simply say that

For instance of size n, multiplication requires cn^2 operations. Hence it is polymonial in time complexity.

Well, that's for that specific algorithm. There are other, faster algorithms, and sometimes that matters, but in general, if instances of a problem can be solved in polymonial time, then the problem is thought of as "easy".

Technically, the problem is in P. (And yes, that's "P" for "Polynomial")

Time complexity of factoring

Factoring seems to be harder. No one has yet found an algorithm that takes only a polynomial amount of time for every instance - for every question - for every number to factor.

There are algorithms that work for only special classes of numbers, but the current fastest general factoring method is called the "General number field sieve"

Don't ask.

The formula for its time complexity is horrendous, but you can read more about that here:

http://en.wikipedia.org/wiki/General_number_field_sieve

There are other, easier to understand methods of factoring, but they all require longer times than this. That's why this one's called "the best" (so far!)

Time complexity of 3-Colouring

Now let's look at 3-Colouring. There are a few different algorithms, but usually what we do is start to colour the nodes, and if we find we get stuck we uncolour the most recent and try something different, and if nothing different works then we backtrack further and try something different for that, and so on.

It seems, though, that when we do this we sometimes end up having to try an exponentially large number of possible colours. Not always - some instances of the problem, some specific graphs, are actually quite easy. If there are no edges, for example, or if every cycle is of even length.

However, for every algorithm we've tried so far, there are cases that require an exponential amount of time.

The algorithms we have for 3-Colouring seem to be Exponential in complexity.

The 3-colouring problem seems to be in Exp, although we don't know for sure.

Verification

But there is an interesting light at the end of the tunnel. While it may take an exponential amount of time to guarantee finding a colouring, it doesn't take that long to verify a colouring. If you claim to have coloured a graph, I can check your claim simply by testing every edge to make sure it doesn't join two nodes of the same colour. Since there can only be up to n^2 edges (actually fewer) this will only take a polynomial amount of time.

In other words, the task of checking a purported solution is polynomial.

Hmm. Thinks: can't solve, but can check. That leads to an interesting "algorithm":

Colour at random
- Check in polynomial time
  - Lather, rinse, repeat

You might not succeed, but it sort-of works, in a non-deterministic sense.

Now, I'm not going to go into the details of what, in this context, is mean by "non-deterministic", but suffice it to say that if you have a problem for which checking a solution to a question is polynomial-time, that problem is said to be in NP.

Quick comment ...

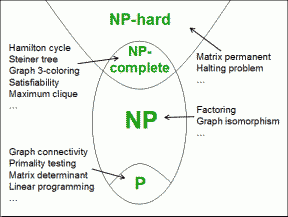
https://www.solipsys.co.uk/new/images/nphard288.png

If a problem is in P then that means there is an algorithm to solve it in polynomial time. Now if you claim to have a solution, I can check it by solving it and comparing my solution against yours. That means I can check your solution in polynomial time.

So every problem in P can have a solution checked in polynomial time.

That means every problem in P is also in NP.

We suspect, but don't know for sure, that there are problems in NP that aren't in P.

That is the question P vs NP

Problem inter-convertability

NP-Complete -> NPC

Links on this page

Site hosted by Colin and Rachel Wright:

Maths, Design, Juggling, Computing,
Embroidery, Proof-reading,
and other clever stuff.

Suggest a change ( <-- What does this mean?) / Send me email
Front Page / All pages by date / Site overview / Top of page

Quotation from
Tim Berners-Lee