Parallelogram Puzzle

Recent changes

Table of contents

Links to this page

FRONT PAGE / INDEX

Subscribe!

My latest posts can be found here:

Colins Blog

Previous blog posts:

Additionally, some earlier writings:

Tagged As Puzzles

A Parallelogram Puzzle

A while ago (March 2nd at 16:28 to be reasonably precise) Ed Southall asked a great question on Twitter:

Can you add a further point
such that joining them up
can make a parallelogram?

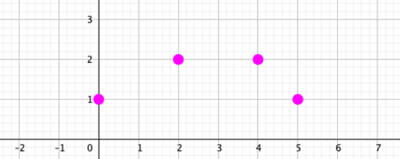
Here's the setup:

The setup ...
Several people chimed in quite quickly, others took a little longer. Some were happy to have found a solution, others were happy to have found two solutions, and then quite a few people started to claim that there were, in fact, exactly two solutions.

That's a pretty bold claim, and of late I've become less sure of myself about these sorts of things. More than once I've made a claim like that, only to have an underlying assumption exposed, leaving me to think more carefully.

Which is good, though sometimes embarrassing, and sometimes even a little painful.

So I wondered, are there really exactly two solutions?

I invite you to go and read the thread, which I've extracted and drawn in chart form.

There you will see some of the solutions, and some of the reasoning. But I promised I'd write more about my thinking, so here it is ...

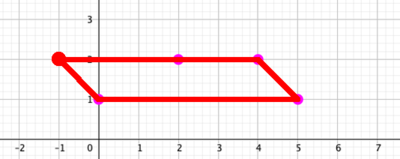
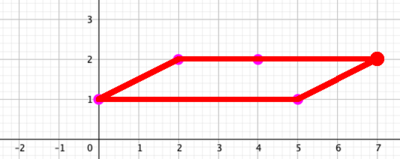
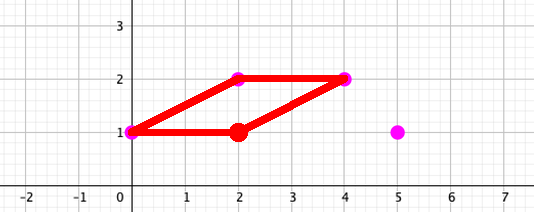
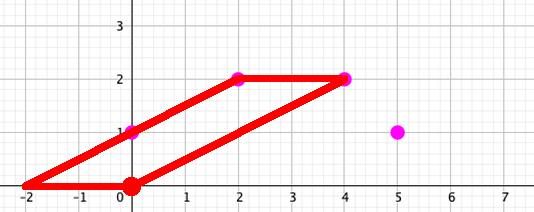
The first solutions

Here are two solutions:

We can see that we've got our four original points, one extra, and then taken what is technically called the "convex hull". Imagine the points are pins in a pinboard, and stretch a rubber band around them. Now all five points lie on the perimeter of the resulting parallelogram, and I'm pretty sure these are the solutions people had when they said there are exactly two.

I'm pretty sure there's no other way to:

Add one point;
Take the convex hull;
Have all five points on the perimeter.

Proving that doesn't seem too complicated, but it would be interesting to nail all the details. That might be harder that you think. Then again, maybe not. I haven't done it.

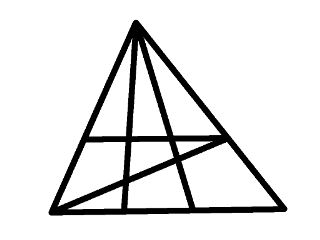
Starting to wonder ...

But then I thought of this puzzle.

Count the
Triangles
The whole point here is that there are triangles with internal lines, and not just the triangles that surround blank space. In particular, we don't insist on using or involving every part of the diagram.

So let's go back and look at the original wording:

Can you add a further point such that joining them up can make a parallelogram?

It's easy to assume that "joining them up" means joining all of them. But if you join every dot to every other dot, you don't get just the perimeter, you also get diagonals, and crossing lines.

So maybe we don't have to involve all the dots, maybe we only need to have three of our original dots plus one extra, and require that they are the corners/vertices of our parallelogram. So maybe the question is:

Add one dot;
Take the convex hull of four of them;
How many ways does this give a parallelogram?

Here's one solution:

https://www.solipsys.co.uk/images/ParallelogramPuzzle_a.png

Convex hull of four points

So how many of these are there?

OK, take any three points and label them A, B, and C. Assume that you are going around the parallelogram cyclically, and where does your next point have to be?

I'm not going to give you a complete list here. Firstly, you probably wouldn't check them, and secondly, it would be a good test of my explanation to see if you can find a few to convince yourself.
Think of B->A as a vector, and add that to C. The point you get to is the fourth point of the parallelogram ... yes, you should check that. Try a few examples.

There are 24 ways to choose 3 points in order from 4, so there should be 24 solutions, assuming no repeats.

But wait! There's more!

So now, what if our parallelogram just needs to "go through" the points, and the points don't necessarily have to be at the corners?

For example, like this:

https://www.solipsys.co.uk/images/ParallelogramPuzzle_b.png

Reaching beyond ...

As you start to explore this you will find infinitely many solutions, but they will, perhaps, come in families, and perhaps you can start to describe those families and get a handle on what's going on.

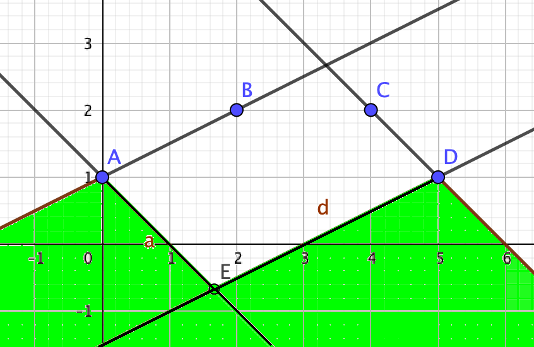
Feedback

Colin Beveridge (Web site) has got in touch and sent me this diagram:

https://www.solipsys.co.uk/images/ParallelogramPuzzle_CB.png

Infinitely many solutions ...

If point E is put anywhere in the green region(s) then we can construct a parallelogram that has all 5 points on the perimeter. It's not the convex hull, but it is a parallelogram that joins all the dots.

<<<< Prev <<<<

Back Of The Envelope COVID19

>>>> Next >>>>

Perception Of Space ...