Recursion Revisited

Recent changes

Table of contents

Links to this page

FRONT PAGE / INDEX

Subscribe!

My latest posts can be found here:

Colins Blog

Previous blog posts:

Additionally, some earlier writings:

Recursion revisited ... a specific example

Some time ago I wrote a post on Thinking About Recursion, and more recently I wrote about a problem concerning the problem of the number of Vertices Required For Cycles. As it happens, the code for that problem is heavily recursive, and provides a great example of using recursion to solve a real problem.

So I thought I'd show you.

The cycle problem

The problem in question is this:

Given a positive integer $C$, what is the minimum number of vertices needed for a graph to contain exactly $C$ cycles?

The function $C{\rightarrow}N$ is now in the OEIS:

https://oeis.org/A333717

But how are values computed?

Counting cycles

The overall strategy is to look at all graphs on $N$ vertices and for each one, count how many cycles there are. Since we will be looking for the minimum number of vertices for a given number of cycles we can ignore graphs that are not connected, and we can ignore graphs that have a vertex of degree 1. So we look at all the non-isomorphic connected graphs of minimum degree 2.

But at its heart, for a given graph we need to count how many cycles it has. Here is the algorithm.

We define routine "count_cycles" which takes a graph in the form of a list of edges. There are more efficient data structures for this algorithm, but for the purposes of describing it we'll stick with this one.

Routine "count_cycles" is a recursive routine.

If there are no edges then the answer is 0 ... there are no cycles.

 
def count_cycles( graph_edges ):

    if not graph_edges:
        return 0

Otherwise we can select an edge. In principle we could find some clever heuristic for choosing the edge, but in practice we simply choose the first edge from the list. Even so, we call out to a routine to make the choice:

 
    selected_edge = choose_edge( graph_edges )

Every cycle either does include this edge, or does not include this edge. So we remove it from the graph:

 
    del graph_edges[ selected_edge ]

Then count the cycles in the graph without that edge. To do that we simply call this routine - this is the first instance of recursion.

 
    cycles_without = count_cycles( graph_edges )

Cycles with this edge
So now we have to count how many cycles there are including this chosen edge. We look at this diagram here on the right, and our chosen edge is the one in red joining the vertices $u$ and $v$, shown in blue.

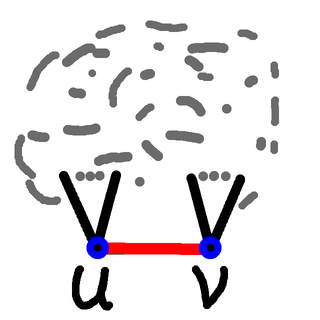
Any cycle that contains this edge $(u,v)$ will then consist of the edge, and a path from $u$ to $v$. So having earlier removed the edge $(u,v)$ we can now count the number of cycles by counting the paths from $u$ to $v$ in this reduced graph.

 
    u, v = vertices_of_edge( selected_edge )
    cycles_with = count_paths( graph_edges, u, v )

We then put the edge back, and return the total:

 
    graph_edges[ selected_edge ] = 1

    return cycles_without + cycles_with

That's how we count the cycles, and all that's left is how to count the paths from $u$ to $v$.

Counting paths

So now we have to write the code to count the paths from $u$ to $v$:

 
def count_paths( graph_edges, u, v ):

If $u$ and $v$ are the same vertex then we have one (degenerate) path:

 
    if u == v: return 1

Paths from $u$ to $v$
Otherwise our path must use one of the green edges shown here on the diagram. Further, since paths (and cycles) can't repeat a vertex, once one of these green edges is used, the other ones can't be used because otherwise we would be returning to vertex $u$. Which is forbidden.

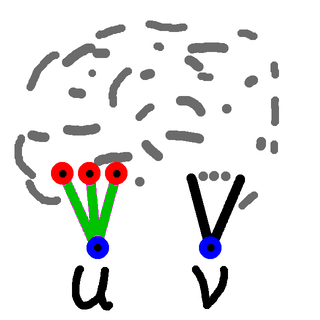
So we can remove the green edges, and for each of the red vertices we then count the number of paths from that to $v$.

So let's get our list of green edges, and remove them:

 
    green_edges = [ e for e in graph_edges if e[0]==u or e[1]==u]
    for edge in green_edges:
        del graph_edges[ edge ]

Then we get our list of red vertices.

 
    red_vertices = [ e[1] for e in green_edges if e[0]==u ] \
                 + [ e[0] for e in green_edges if e[1]==u ]

The total number of paths from $u$ to $v$ is the total number of paths from the red vertices to $v$. So we take that total by a recursive call to this same routine:

 
    total = 0
    for red_vertex in red_vertices:
        total += count_paths( graph_edges, red_vertex, v )

Finally, we put all those edges back, and return our result:

 
    for edge in green_edges:
        graph_edges[ edge ] = 1
    return total

def count_paths( graph_edges, u, v ): if u == v: return 1 green_edges = [ e for e in graph_edges if e[0]==u or e[1]==u ] for edge in green_edges: del graph_edges[ edge ] red_vertices = [ e[1] for e in green_edges if e[0]==u ] + [ e[0] for e in green_edges if e[1]==u ] total = 0 for red_vertex in red_vertices: total += count_paths( graph_edges, red_vertex, v ) for edge in green_edges: graph_edges[ edge ] = 1 return total def count_cycles( graph_edges ): if not graph_edges: return 0 selected_edge = choose_edge( graph_edges ) del graph_edges[ selected_edge ] cycles_without = count_cycles( graph_edges ) u, v = vertices_of_edge( selected_edge ) cycles_with = count_paths( graph_edges, u, v ) graph_edges[ selected_edge ] = 1 return cycles_without + cycles_with

Summary

So here is the code complete. The routine "count_cycles" calls itself recursively, and also calls "count_paths". In its turn the routine "count_paths" calls itself recursively, and we're done.

With any recursive routine we should always ask: How do we know the recursion bottoms out?

The answer in this case is that in every call the number of edges decreases, is a whole number, and cannot go below zero. Because of that, in each case the call tree has to terminate.

And the code isn't that big, nor that complicated. This is the power of recursion when appropriately applied.

End Notes

This is not intended to be especially efficient code, nor is it particularly good Python code. That's not the purpose (in this case). The final version was more efficient, but less clear due to the modifications made for that efficiency.

Even so, I hope the algorithm, and how the recursion works, is clear.

<<<< Prev <<<<

Vertices Required For Cycles

>>>> Next >>>>

When The Text And Html Disagree ...