The Other Rope Around The Earth

Recent changes

Table of contents

Links to this page

FRONT PAGE / INDEX

Subscribe!

My latest posts can be found here:

Colins Blog

Previous blog posts:

Additionally, some earlier writings:

2019/01/15 - The Other Rope Around the Earth ...

The well-known "Rope Around the Earth" problem is lovely, and, as I say, well known. But some time ago David Bedford mentioned another rope around the Earth problem. A different rope around the Earth problem. And it goes like this.

Our protagonist has gone onto the internet and purchased 40 million metres of rope, as you do, and then wandered around the Earth, stretching it out behind. As you do. The expectation was that it would exactly encircle the Earth, since the original definition of the metre was that the distance from the North Pole to the Equator, through Paris, should be 10 million metres.

Alas, things didn't quite work out, and there was a six metre excess.

Well, our protagonist didn't want to cut it, because it was expensive, and didn't want to tie a knot, because that would be ugly. So they fused the ends together, and wondered what to do with the slack.

In the original problem it was distributed evenly around the Earth by propping it up a fixed distance everywhere, and the question is: How high will that be?

But that's silly. Having gone all the way around the Earth once to put the rope there in the first place, who would go around a second time to prop it up?!?

No, let's just get a tall tent-pole and prop it up here.

Now a three metre tent-pole won't do the trick, because the rope will run up to it on one side, go up, come down, and go on its way, the 6 metres of slack being used.

So the pole has to be taller than 3 metres. But how much taller?

Unrealistic, I know, but we are in puzzle world.
We are, of course, assuming that this is the kind of rope we find in physics problems/puzzles, it's light and inextensible. So it won't stretch, and when we pull tight, it doesn't sag.

So there is the question.

How high must the
tent pole be?

But the meta-question is this: Can you make the calculations simple enough to do in your head (or on a sheet of paper). No calculators.

How close can you get?

The answer continues here, but I strongly urge you to have a play with it first. For one thing, you might get a better answer! For another, if you've played with it for a bit you can follow along more easily.

However, here we go ...

The calculation

So here is the picture we have. The rope stretches around the world, but then at some point leaves the surface and travels in a straight line (because it doesn't sag). To the top of the pole. From there it again travels in a straight line back to the Earth;s surface, and carries on around the Earth to complete its journey. And this is 6 metres longer, in total, than simply staying on the surface.

That means that the tangent on each side must be 3 metres longer than the arc length, so we have this equation:

$R\tan(\theta)-R\theta=3$

We can divide through by $R$ to get:

$\tan(\theta)-\theta=3/R$

Now the problem with this is that it's a transcendental equation, mixing $\theta$ and $\tan(\theta)$, and that means we don't have a simple way to solve it exactly. We can solve it numerically, but even if we do that, it's useful to have a "good guess" to start with. So let's have a stab at solving it, at least approximately.

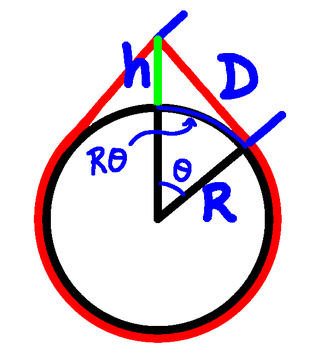
We start with the equation we had from the "Distance to the Moon" calculation, that provided $h$ is not too large (whatever that means), $D^2\approx 2hR$, where $D$ is the distance to the horizon, $R$ is the radius of the Earth, and $h$ is the height from which we are making the observation. We rearrange that to make $h$ the subject:

$h\approx\frac{1}{2}D^2/R$

We also know from the Elementary Estimates page that when $\theta$ isn't too large (again, whatever that means), then $\tan(\theta)\approx\theta+\theta^3/3$.

Substituting that into our equation about the length of the rope:

$\tan(\theta)-\theta=3/R$

we get:

$\theta^3/3\approx 3/R$

Multiply through by $3$ to get:

$\theta^3\approx 9/R$

Yes, it should perhaps be $R\tan(\theta)$, but it is close enough.

That's well and good, but we don't really want $\theta$, we want $h$. But our equation for $h$ uses $D$, and $D$ is roughly $R\theta$.

So multiply both sides by $R^3$ and we get:

$R^3\theta^3\approx 9R^2$

which is:

$D^3\approx 9R^2$.

Raise both sides to $2/3$ to get:

Yes, I've slightly pulled a fast one by squaring the 9.

$D^2\approx {81}^{1/3}R^{4/3}$

Now we have our previous equation:

$h\approx \frac{1}{2}D^2/R$

We substitute for $D^2$:

$h\approx\frac{1}{2}{81}^{1/3}R^{4/3}/R$

Simplify:

$h\approx\frac{1}{2}{81}^{1/3}R^{1/3}$

Bizarrely, now write $1/2$ as $(1/8)^{1/3}$ and we have:

$h\approx(\frac{1}{8})^{1/3}(81)^{1/3}R^{1/3}$

which simplifies to:

$h\approx\left(\frac{81}{8}\right)^{1/3}R^{1/3}$

But $\frac{81}{8}\approx 10$, so we have:

$h\approx (10R)^{1/3}$.

We know that $R\approx 6.4\times 10^6$, so we have:

$h\approx (64\times 10^6)^{1/3}$.

Which is 400.

Which is nice.

Refining the numbers

We've made approximations all over the place, but most have been the small angle approximations, and they're pretty good - we'll see what $\theta$ is in a moment.

The main approximation was to replace $\frac{81}{8}$ with $10$, an error of 1.25%. When we take the cube root, the error due to substitution is then about 0.41%, so our answer should be 0.41% bigger. That makes it $h\approx 401.64$, although certainly some of the decimal places are not justified.

So our final answer is $401.64$ metres.

So what are the actual numbers?

Solving numerically we get $\theta\approx 0.01120332437$, and so $D=R\tan(\theta)$ is about $71704.276$. Now we compute $h$:

$(R+h)^2=D^2+R^2$

$h=\sqrt{D^2+R^2}-R$

That comes out as $h=401.667...$, as compared with our answer of $401.64...$

That'll do.

How good are the approximations?

So just how good are the approximations? We can have a look at the value of $\theta$. Our numerically derived value is $0.01120332437$, but the approximation is $\left(9/R\right)^{1/3}=0.01120351...$, so they agree to 6 decimal places, or 5 significant figures. That's pretty good. Then at that value of $\theta$ we can also compare $\tan(\theta)=0.0112037931200...$ with $\theta+\theta^3/3=0.011203793096...$, agreement to nine decimal places, or, as Rob Low says:

"... more decimal places than a
sane person would consider relevant."

That's why our value for $h$ is so close - the approximations are good ones.

And finally ...

Rob also suggested a slightly differ route to the answer. My calculation was done in my head, and I was able to use the formula for the distance to the horizon, because that was something I'd done earlier. And just as in the case of the Radius Of The Earth Part Two, that biased me to a particular way of working.

This looks longer and more complicated than it really is. I've included all the details, expanding heavily on what Rob sent me for the sake of making it all very clear as to where everything is coming from. Sometimes you need to do that when explaining something for someone else to follow - this level of detail is rarely necessary when it's your own line of thought, or when you're working with someone who has a similar background.
Rob suggests the following - relying heavily on the approximations in the post on Elementary Estimates:

From the diagram:

$\cos(\theta)=R/(R+h)$
- so $R+h=R/\cos(\theta)$
$\cos(\theta)\approx 1-\theta^2/2$
- so $1/\cos(\theta)\approx 1+\theta^2/2$
  - so $R/\cos(\theta)\approx R(1+\theta^2/2)$
Combining: $R+h\approx R(1+\theta^2/2)$
- so $h\approx \frac{1}{2}R\theta^2$

For a reason not currently apparent, cube both sides:

$h^3\approx \frac{1}{8}R^3\theta^6$ (1)

Now, to take up our 3 metres slack on each side we need:

$R\tan(\theta)=R\theta + 3$
- so $\tan(\theta)=\theta + 3/R$
$\tan(\theta)\approx\theta+\theta^3/3$
- so $\theta+\theta^3/3\approx\theta + 3/R$
  - so $\theta^3/3\approx 3/R$
    - so $\theta^3\approx 9/R$

Square both sides to get: