The Other Wrapping The Earth Problem

Recent changes

Table of contents

Links to this page

FRONT PAGE / INDEX

Subscribe!

My latest posts can be found here:

Colins Blog

Previous blog posts:

Additionally, some earlier writings:

The Other "Wrapping the Earth" Problem

If you've been reading the previous posts you'll know the drill. This is a brief recap ...

Our friend once again has too much to drink, and once again indulges in a little late night internet shopping. This time, however, it's fuelled by curiosity, having discovered that there's a material that is infinitely stretchy, but which always retains its area. So while you can stretch it one direction, it will shrink in another.

We know the Earth's circumference is 40 million metres, so our friend purchases some 510 million million square metres of this wonderful material, expecting that it will be about the right amount to wrap up the Earth, and goes off to bed.

It takes some time for the order to arrive - next day delivery wasn't available from this vendor - but when it does arrive our friend goes to it and heroically wraps the entire Earth, only to discover that there is slightly too much material. Just one square kilometre.

One million square metres.

Last time we looked at solving the problem by propping it up the same height everywhere, but that really is a lot of work. Much easier just to get a tent-pole and prop it up in just in one place.

How high will that have to be?

The sums ...

The Yurt (in blue)
So we stick our tent-pole under the wrapping and start to lift it, and in doing so we create a sort of yurt. The height of the pole is $h$ and the "slope height" of the yurt is $D$. If the tent-pole is at the North pole then the yurt "touches" down at some latitude, which in turn defines a circle around the Earth. So the straight line, through-the-Earth radius of the rim of the yurt is $r$, shown in purple on our diagram.

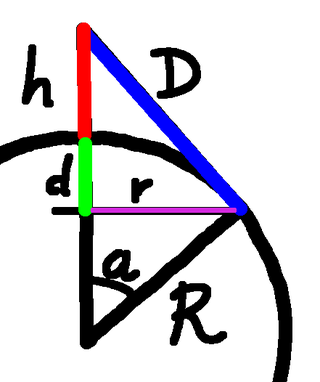
As always, the radius of the Earth is $R$.

The area of the spherical cap that the fabric has been lifted from is $\pi(r^2+d^2),$ and the area of the "Yurt" is $\pi rD$. The first is from Archimedes Hat Box Theorem, and the second requires a little work, but is the formula for the area of the curved surface of a cone.

So where do we begin? There are lots and lots of right-angled triangles in this diagram, so we could start by writing them down:

$R^2+D^2=(R+h)^2$
$r^2+(d+h)^2=D^2$
$r^2+(R-d)^2=R^2$

and so on. I did that for ages and then tried chasing things down. But in the end, here's the calculation that worked for me.

Area of the cap is $\pi(d^2+r^2)$
Area of Yurt is $\pi rD$

We use the following abbreviations:

$c = \cos(a)$
$s = \sin(a)$
$t = \tan(a)$

And so:

$c = R/(R+h)$
- ... hence $h=R\left(\frac{1}{c}-1\right)$
$d = R(1-c)$
$r = R s$
$D = R t$
Yurt minus Cap:
- $\pi\left(rD-(d^2+r^2)\right)$
- $\pi\left[Rs\cdot Rt - R^2(1-c)^2-R^2s^2\right]$
- $\pi R^2\left[(1-c^2)/c - 1 + 2c - c^2 - s^2\right]$
- $\frac{1}{c}\pi R^2(1+c^2-2c)$
- $\pi R^2\frac{1}{c}(1-c)^2$

Assuming $a$ is small, we can use the small angle approximation to simplify this. We use $1-c\approx a^2/2$ and $\frac{1}{c}\approx 1$ and when the dust settles we have:

Yurt minus cap:
- $\Delta \approx \pi R^2 a^4/4$

No, that's neither immediate nor obvious, but it yields to simple algebra. Really, try it.

Now we return to $h=R\left(\frac{1}{c}-1\right)$, substitute $c\approx 1-a^2/2$ and simplify, and we end up with:

$h\approx R a^2/2$

Square that:

$h^2\approx R^2 a^4/4$

We can see the right-hand side of that in our expression for $\Delta$, so our result is:

$\Delta \approx\pi h^2$

My reaction to that was - What? Really?

Using the result

Firstly, it amazed me somewhat that the result doesn't rely on the size of the Earth. In fact it does, but that's hidden in the small angle approximation, so we do need the Earth to be big enough. But even so, the result doesn't rely on the size of the Earth, so we can simply do the sums to find the height:

$h \approx \sqrt{\Delta/\pi}$

Our required $\Delta$ is one million, and the square root of that is one thousand. Using a calculator we have $\sqrt{1/\pi} \approx 0.564$ and so we have our result:

$h\approx 564$ metres.

It's worth checking that the small angle approximations are valid. So what is $a$? Working backwards we find that $a\approx 0.0133$ radians, or about $0.76$ degrees. That's small enough.

Can we avoid the calculator?

It depends on what you know. I remember that $\sqrt{1/3}\approx 0.577$, so that's close to $\sqrt{1/\pi}$. We can get closer by remembering that $\pi$ is about 5% bigger than 3. We're taking a square root and dividing, so our answer should be about 2.5% smaller than 577. Taking 2.5% is dividing by 10, then by 4, so that's 14.4 (ish) and we subtract that from 577 giving a rough, back-of-the-envelope calculation of about 562 or 563.

That's pretty close.