Thinking About Recursion

Recent changes

Table of contents

Links to this page

FRONT PAGE / INDEX

Subscribe!

My latest posts can be found here:

Colins Blog

Previous blog posts:

Additionally, some earlier writings:

Recursion ...

It has been said that there are two hard problems in computing:

Cache Invalidation,
Naming Things, and
Off-By-One Errors.

Well, that's certainly true when you get into the practice of programming. But on the way to becoming a programmer we find that there are multiple levels of enlightenment.

Variables

It's important to realise that variables in mathematics and variables in programming have a lot in common, but they are not the same thing! In mathematics, sometimes a "variable" is a place-holder for a value one may choose arbitrarily from a collection, and which is then used in some process, while sometimes a "variable" is a place-holder for a value that we do not know, but which is stated to satisfy some requirements and is subsequently to be determined. In fact, sometimes we find that there is no value satisfying the requirements we have placed on the variable, so in a sense it doesn't exist at all!
The first level is to understand that a string of letters and other symbols can represent a value, and that the value represented can be changed. These are variables, and when I've been teaching people to program sometimes I see the light dawn when they realise that a variable name is like a box with the name on the outside. The box can hold something, we can look at it, test it, take a copy of it, or remove it and replace it with something else.

A variable has a name, and it holds a value.

Some people seem never to actually get that idea, and mistakes they subsequently make can often be traced to a non-understanding of this. But most people seem to get the idea, either immediately, or after a small amount of practice.

It has to be said, though, that in some modern languages the situation starts to get murkier. Sometimes a variable doesn't actually hold the value, it pretends to hold the value, and instead holds a pointer to the value, and the value itself is somewhere else. Then more than one variable can point to the same value. Some languages, Python for one, hide this implementation detail from you, so when you mutate the value via one variable and discover that the value "in" another variable has also changed, that can be a little surprising.

And it gets even more complicated, but I'm not going to go there.

The Function

A "function" in mathematics is a different beast from a function in programming. In mathematics a function doesn't even need to have a rule to tell you what it is, whereas in programming a function tends to be a process, a series of steps, that will be performed several times in different locations in the code, and hence there is value in abstracting it from the code and enable it to be called from different places.
Many students (and people in general) when told "Consider a function" immediately assume there is a rule to define it. Often they have only ever been shown examples where such a simple and elegant definition exists. To a mathematician, though, when one says "Consider a function" the image that comes to mind is simply

"Blob here,

blob there,

arrow between."
There need not be a simple formula, or even a means to compute the value for a given input. Until we are told otherwise, pretty much the only thing we know about a function in mathematics is that each item in the domain is assigned one (and only one) item in the range.
The second level of enlightenment is the function. For some people it seems to be fairly straight-forward. A function is a sort of "black box". You feed it things, it gives you things back.

Actually, sometimes you don't actually give it anything and it gives you back a value anyway, and sometimes it doesn't give you anything back! Yes, a "function" in computing can be a interesting beast, and is definitely different from a mathematical function.

This can be even further complicated by the fact that sometimes you want your black box to have a memory, and in those cases even if you feed it the same thing multiple times you get different things given back to you.

But in essence, in computing a "function" is a thing you refer to. You give it values (most of the time) and it does something, which might include giving you something back. Seems straight-forward, but for some people it just remains a complete and total mystery as to what's going on at all.

Interestingly, I've found that some people have the same stumbling block in mathematics. They can "do sums" but the abstract concept of a "function" seems to defeat them. In some cases, for some people, it seems simply to be that they've never been exposed to functions in general and have always just dealt with formulas, but some people seem never really grasp the idea of a thing that takes things and gives you back things. Put like that it's perhaps not so difficult to see why they might have problems.

Even so, for some people,"functions" are their Waterloo in the field of programming.

Recursion

Now we come to the third level of enlightenment: recursion.

It seems to me, speculating idly and with no research to back me up, that recursion has similar conceptual challenges as Mathematical Induction and Proof By Contradiction. Perhaps the parallel with Mathematical Induction is fairly obvious, perhaps Proof by Contradiction less so, but stay with me for the moment.

What is recursion?

It might be worth noting here that some (most?) early programming languages (specifically Fortran 77, for example) didn't allow a function to call itself - recursive calls were explicitly forbidden.
In recursion we define a function, but in computing the value to be returned, the function is allowed to call itself. For some people this is simply incomprehensible, or nonsense, because how can a function that is not yet defined somehow use itself to compute itself?

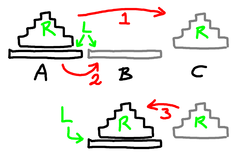
A similar problem arises with Mathematical Induction. Here we want to prove a proposition, but somehow we can magically use the truth of the proposition to prove the proposition. That seems to be obvious nonsense. How can we make sense of it?

A specific example: The Towers of Hanoi

So let's take a specific example, solving the Towers of Hanoi.

We have three locations, A, B, and C, and a collection of disks of different sizes. Currently they are all stacked up in location A, and we want them instead to be in location B. But there are rules.

Firstly, we can only move one disk at a time. And secondly, we may never put a larger disk on a smaller disk.

Playing randomly with one of these for a bit shows that there is obviously some way of doing it, and some structure to the solution, but it would be nice to have a rigorous solution. And there is ... it goes like this.

If there's only one disk then move it where you want it to go. Done.

If there's more than one disk, think of it as the bottom-most disk, L, and the remainder, R. We want to move L+R from location A to location B, so we move R to C, then move L to B (our desired final location), and finally, move R to sit on top of L in location B.

But hang on, R might have lots of disks, and you haven't told me how to move them!
- You can use the same instructions to move R from where it is to where I want it.
But you still haven't actually told me how to move R !
- Yes I have ...
No you haven't!
- Yes I have ...

.... and so on.

So how does this work?

The basic idea is this. Start by showing how to solve the simplest possible case. With this problem we've shown how to solve the problem when there is only one disk.

Now consider any case, and assume (this is the bit some people find tricky) that we can solve all cases that are in some sense "simpler." If we can show how to break down the case we're trying to solve into a combination of simpler cases, then we're done.

And that's what we've done above. We're confronted with N disks, and we assume that we can solve the Towers problem when there are fewer than N. We then observe that if we move N-1 disks out of the way (and we can, by assumption), move the last disk, then move the N-1 again (and again, we can), then we're done.

So to make this work we need a few things:

A set of "simplest" examples;
A concept of one instance being harder than another;
A finite path from an instance back to one of the simplest;
A method of solving each instance given solutions to the simpler ones.

Some more specific examples

This is pretty much the same as "Proof by Induction" in mathematics.
So here are some simple examples. In each case you'll see that the code picks off the "obvious" simplest cases. Then after dealing with those we compute the desired value by using a "simpler" case.

def factorial(n): # We are assuming n is an integer if n<0: return 'Error!' if n==0: return 1 return n * factorial(n-1)

The "factorial" is a classic example of recursion. Normally written as n!, the factorial of n is the product of all the integers from 1 up to n inclusive, with 0! defined to be 1 (for reasons we won't go into here).

So here we compute n! by saying that if n is zero then the answer is 1, otherwise we compute (n-1)! and multiply by n. In truth you would never compute factorial like this in real life, but it's a reasonable example of how the process works.

def fibonacci(n): # We are assuming n is an integer if n<0: return 'Error!' if n==0: return 1 if n==1: return 1 return fibonacci(n-2)+fibonacci(n-1)

This code follows the usual definition of the Fibonacci numbers, where F(0)=F(1)=1, and after than each Fibonacci number is the sum of the two preceding numbers. The problem with this in practice is that it takes exponential time to compute! Using this routine to compute Fib(30) requires well over a million calls.

There are faster and practical ways, but this routine is here to demonstrate recursion. If you want to compute the Fibonacci numbers, don't do it like this.

Really. Don't.

def binary_search( K, V, L, U ): # K is a thing to find # V - a sorted list of things # L, U - non-negative integers # We assume that if K is in V, # and is at location i, then # L <= i < U if not L<U: return 'Not Found' if L+1 == U: if V[L] == K: return L else: return 'Not Found' m = floor( (L+U)/2 ) if K < V[m]: return binary_search(K,V,L,m) else: return binary_search(K,V,m,U)

This is a more complex, but fairly realistic example. We are conducting a "binary search" for a particular item - the "key" - in a sort vector of items.

Imagine you have a bookshelf with books ordered by title, and you're looking for one in particular. You look in the middle and if what you're looking for is earlier than the book there, move left, otherwise more right.

Here we have a list of objects, V, sorted from least to greatest, and we're looking for a specific item, K. The routine takes the key, the list, and a range [L,U) in which the item occurs, if it's there at all.

The "lower" bound is inclusive, the "upper" bound is exclusive.

Let's see how the code is structured.

If the array is empty then the item isn't found, obviously. If there is only one item in the list then either our key is there or it isn't, and we return the appropriate result.

For those of you who know about this, m should be computed as
# Using integer arithmetic m = L+((U-L)>>1)
to avoid the possibility of integer overflow. If you don't know about this, don't worry. If you want to know more about this, start here:

https://www.google.co.uk/search?q=mid-point+overflow

Otherwise we compute a "mid" point and think about the list being divided there. We ask how the value at that mid-point compares with our key, and then search only the appropriate half. The detail is tricky, but that's what (some) programmers do.

Returning to mathematics

The connection between recursion (in programming) and mathematical induction is reasonably straight-forward. In each case we deal with the instance in front of us by assuming we can do simpler instances, and then using them to solve the one we have. What is the connection with Proof by Contradiction?

This section is optional. Some readers have declared it impenetrable, others have found it so obvious as to be pointless. Be warned, this section is not a simple read.
In its simplest form, suppose we have a proof by induction of some fact. That means that we have proven our fact for the case n=1, and we have shown that if it's true for n=k then it's also true for n=k+1. How do we now know that it's true for all n ?

Some have offered the visualisation of an infinite row of dominoes. They say that if you show that each will cause the next to fall, and you knock over the first one, then they will all fall. The problem is that people then seem to talk about things becoming true. The analogy has its uses, but can be misleading.
Suppose there is some n for which our proposition fails, and consider the smallest such n. We will derive a contradiction.

Our first failure can't be at n=1 because as part of a proof by induction we have proven our proposition is true in that case, so that means n>1.

Now consider n-1.

Since n is the first failure, the proposition is true for n-1. Because we have a proof by induction, we have a proof that if it's true for n-1 then it's true for n.

So it's true for n.

So assuming it fails somewhere leads to a contradiction. Thus we have used Proof by Contradiction to show that the steps of Proof by Induction suffice to show that something is true.

Well, not quite. We've also used that there's a smallest case for failure, so that uses the Well Ordering principle, and so it goes on. Suffice it to say that these things are all connected, and some things are more obvious to some people, while other things are more obvious to other people.

In short, it can be complicated, and when you first meet the ideas they can be a little daunting, and not at all obvious. For some people (perhaps nearly all of us!) it's only with time that they become easy and "obvious."