Volume Of A Sphere

Recent changes

Table of contents

Links to this page

FRONT PAGE / INDEX

Subscribe!

My latest posts can be found here:

Colins Blog

Previous blog posts:

Additionally, some earlier writings:

This page has been
Tagged As Maths

Volume of a Sphere

Yesterday (as I type this) Fermat's Library on Twitter tweeted this:

It was only 282 years ago that Euler presented in his textbooks the exact formula for the volume of a sphere.

Click here to see the original

Then there was an image with the actual formula: $V=\frac{4}{3}{\pi}r^3$.

Over 12 thousand people "Liked" the tweet, but someone said:

... how would you go about proving this one?

So here is how we can prove it.

Volume of a cone

Firstly, think about a cube. We can think of the cube as six pyramids put together with their apexes meeting in the middle. The apex of each pyramid is in the exact centre of the cube, so if the cube has a side length of 1, then the pyramids will have to have "height" $\frac{1}{2}$. Then because there are six identical pyramids we can conclude that each pyramid is one sixth of the volume of the cube.

So a square-based pyramid of side length 1 and height $\frac{1}{2}$ has a volume of $\frac{1}{6}$.

Imagine doubling the height of the pyramid. That would double the volume, so now the volume is $\frac{1}{3}$.

So a square-based pyramid of side length 1 and height 1 has a volume of $\frac{1}{3}$.

A few people have asked about this. Imagine taking your pyramid, or indeed, and shape, and think of an approximation made up of tiny cubes. Now double each cube in height. Doing so doubles the volume of each little cube, and therefore doubles the volume of the whole thing. But it also doubles its height.

Generalising this argument, we can see that scaling by some factor in one direction increases the volume by that factor.

You may need to think about that for a bit ...

Thinking about scaling this vertically:

If we multiply the height by 5, the volume is now $\frac{5}{3}$;
- If we multiply the height by 8, the volume is now $\frac{8}{3}$;
  - If we multiply the height by $h$, the volume is now $\frac{h}{3}$,
    - which can also be written as $\frac{1}{3}h$.

Now think about scaling the base. If we make the edges of the base twice the size, the area of the base is four times the size, and the volume similarly increases by a factor of 4. Thinking carefully about this we get the following:

If the area of the base of a pyramid is $A$,
- and the height is $h$,
  - then the volume is $\frac{1}{3}Ah$.

This isn't limited to square-based pyramids, though, it's true of every pyramid and every cone. Take any shape of area $A$ in the plane, and any point above it. Join that point to every point on the rim of the shape to make a cone-like "thing", and the volume of that resulting "thing" is $\frac{1}{3}Ah$.

Comparing volumes

Consider two identical stacks of coins. The volumes of the stacks are the same, and this remains true even if you slide some of the coins sideways to make one of the stacks "wonky".

Using that as our inspiration we introduce "Cavalieri's principle" which says this:

Given two things standing on a table, if every slice taken parallel to the table results in cross-sections of the same area, then the two things have the same volume.

Basically, if you have two stacks of things, and at every height the areas are the same in each, then the volumes are the same. You can play with an interactive version of the idea here:

Cavalieri's Principle
(opens in a new tab or window)

So in some cases we can compare volumes as follows:

Put the two items on a table;
- Take a slice at some height;
  - Measure the resulting area of each cross-section;
    - If they are always the same,
      - the two items have the same volume.

(And yes, that was literally a re-statement of Cavalieri's Principle.)

The Cone, the (Hemi)-Sphere, and the Cylinder

Perspective view

Now pick some value, $R$, which we are going to use as a radius for a cone, and hemisphere, and a cylinder. We take a hemisphere, cone, and cylinder, and arrange them in a line, with the cone "inverted". This image here has them sliced vertically to show a cross-section, as that's how we will be thinking about them

So let's have a look at that cross-section.

Taking a "side on" view here, seeing the hemisphere, inverted cone, and cylinder, all from the side, and we have taken a slice through them all at some arbitrary height $h$. The three objects here are all of height $R$ and radius $R$, so the sides of the cone are at 45 degrees to the table on which they rest (even though in my rough, hand-drawn diagram they don't look like it).

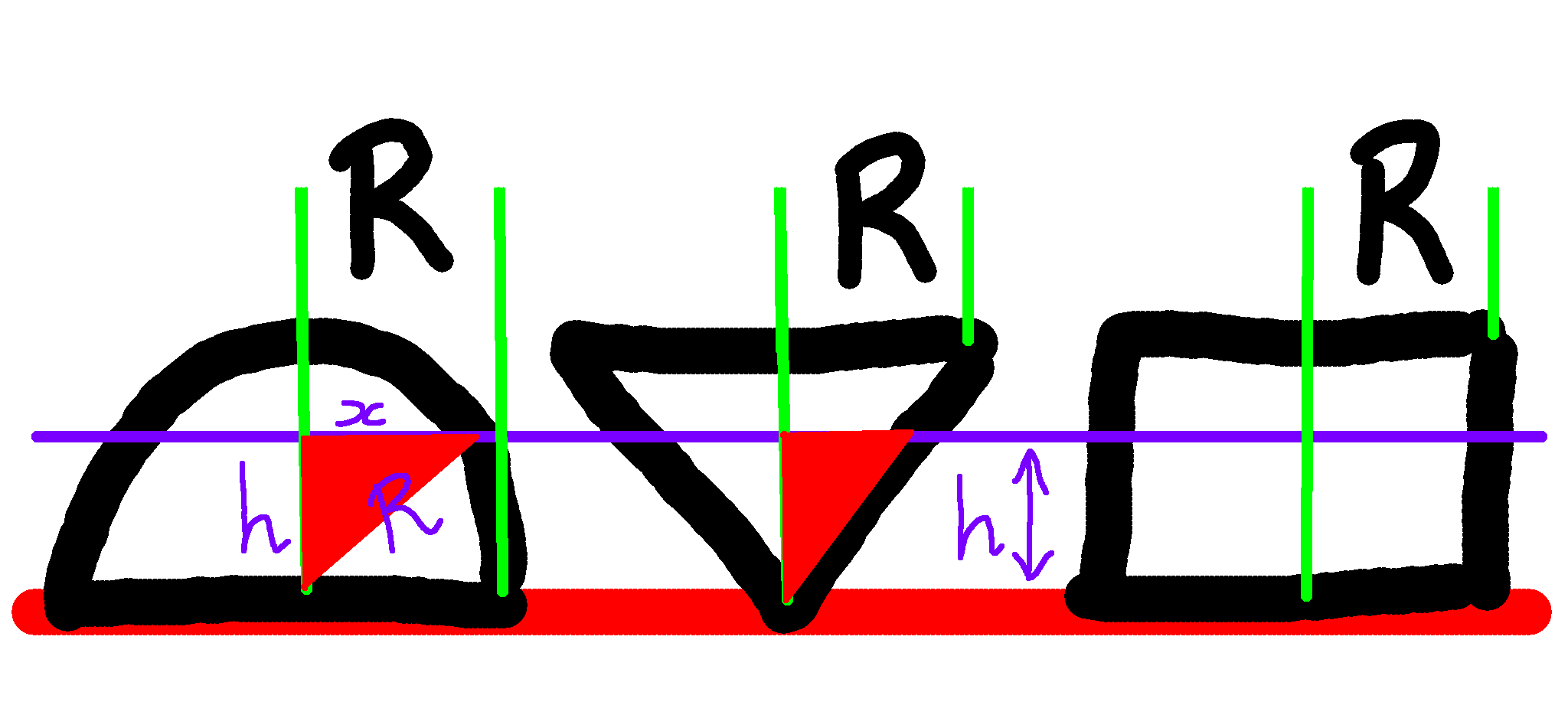
Hemi-sphere, Cone, and Cylinder

We know that taking a slice through the cylinder will result in a circle of radius $R$, and hence area ${\pi}R^2$. The slice through the cone will also give a circle, and when we realise that the red triangle is (despite the drawing!) a 45-45-90 triangle, we can see that the radius of the circle will equal the height of the slice, and so the radius of the slice in the cone will be $h$, the height of the slice. So its area will be ${\pi}h^2$.

In the case of the slice through the hemisphere, that will also be a circle, and we can compute its radius (and hence area) by using our old friend, Pythagoras' Theorem. We have a right-angled triangle with hypotenuse the radius of the hemisphere, hence $R$. The height, and hence one short side, is $h$, so we have the equation:

$h^2+x^2=R^2$

Rearranging that we have $x^2=R^2-h^2$ and so the area of the slice section is ${\pi}(R^2-h^2)$.

Combining the results

Now for the pay-off. Looking at the slices through the hemisphere and cone, their total area is:

${\pi}(R^2-h^2)\;+\;{\pi}h^2$

But that simplifies to be ${\pi}R^2$, which is the area of the slice of the cylinder.

So using Cavalieri's Principle;

the volume of the hemisphere
- plus the volume of the cone
  - equals the volume of the cylinder.

The cylinder has volume ${\pi}R^3$, because that is the height times the area of the base. The cone has volume $\frac{1}{3}{\pi}R^3$, being one third of the base area times the height. So the volume of the hemisphere is the difference, which is $\frac{2}{3}{\pi}R^3$.

Therefore the volume of the full sphere is twice that.

Thus the volume of a sphere of radius $R$ is $\frac{4}{3}{\pi}R^3$.